Ряды с неотрицательными членами

Гармонический ряд.

Рассмотрим ряд

                                                      (4)

очевидно, он расходится. Но и ряд

 ,                                                 (5)

составленный из обратных величин соответствующих членов ряда (4), также расходится. Чтобы доказать расходимость ряда (5), воспользуемся оценкой

.

Значит, в сумме первых  слагаемых

каждая из скобок больше ½; количество скобок можно взять любым, подобрав лишь число m. Отсюда следует, что последовательность частичных сумм является неограниченной. Следовательно, ряд (5) расходится.

Ряд (5) называется гармоническим рядом.

 

Критерий Коши сходимости ряда.

Необходимый признак сходимости числового ряда.

С бесконечным рядом (1) связаны ряды вида , называемые остатками ряда (обозначается ). Справедливо следующее утверждение.

Утверждение 1.  Числовой ряд (1) сходится тогда и только тогда, когда для любого  сходится его остаток .

Доказательство.

Достаточность. Если для любого   остаток   сходится, то  он сходится и при . Но  – это и есть исходный ряд.

Необходимость. Если ряд (1) сходится, то существует 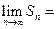. Но  частичная сумма  ряда  имеет вид . Величина  не зависит от . Кроме того,  при . Поэтому существует . Утверждение доказано.

Итак, исследование сходимости ряда и исследование сходимости любого его остатка – эквивалентные задачи. Значит, при изучении сходимости ряда можно рассматривать его, начиная с некоторого номера. Это не влияет на сходимость ряда, изменится лишь его сумма.

Напомним формулировку критерия Коши для числовых последовательностей:

последовательность  сходится тогда и только тогда, когда

.

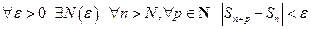Здесь . Так как сходимость последовательности частичных сумм означает сходимость ряда, то сформулируем критерий Коши для рядов.        

Теорема. Числовой ряд (1) сходится тогда и только тогда, когда

.

Следствие. (Необходимый признак сходимости ряда). Если числовой ряд сходится, то его общий член стремится к нулю: .

Действительно, из критерия Коши при 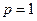 получаем неравенство , выполняющееся . Это и значит, что .

Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда. Можно указать расходящийся ряд, для которого выполняется условие . Например, для гармонического ряда  очевидно справедливо равенство , т.е. общий член ряда стремится к нулю, но как мы видели выше, этот ряд расходится.

Необходимое условие можно сформулировать и как достаточный признак расходимости.

Теорема (достаточный признак расходимости). Если последовательность  не является бесконечно малой, то ряд (1) расходится.

Таким образом, доказанная теорема иногда позволяет, не вычисляя частичной суммы S_n, сделать заключение о расходимости того или иного ряда. Например, ряды , ,  и  расходятся, так как соответствующие последовательности  не является бесконечно малыми:

,  не существует, .

 

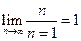Ряды с неотрицательными членами.

Если известно, что все члены ряда  имеют, начиная с некоторого номера, постоянный знак, то исследовать его сходимость проще, чем в общем случае. Это связано с простым критерием сходимости для таких рядов. Для простоты предположим, что все .

Отсюда вытекают три простых свойства рядов с неотрицательными членами.

· Последовательность частичных сумм неотрицательна, т.е. .

· Последовательность частичных сумм монотонна, т.е. .

· Для того чтобы последовательность частичных сумм сходилась необходимо и достаточно, чтобы она была ограничена:

 сходится .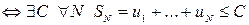

Используя последний факт, легко доказать следующие признаки сходимости числовых рядов с неотрицательными членами.

 

Признаки сравнения

Теорема (первый признак сравнения). Пусть  для всех . 1. Если ряд  сходится, то сходится и ряд .

2. Если ряд  расходится, то расходится и ряд .

Доказательство. Если  для всех , то очевидны неравенства .

1. По условию, ряд  сходится. Значит, по приведенному выше критерию . Но тогда и , значит, ряд  тоже сходится.

2. Пусть ряд  расходится. Тогда если бы ряд  сходился, то из уже доказанного утверждения должен был бы сходиться и ряд , что противоречит условию. Следовательно, расходится и ряд .

Пример. Исследовать сходимость рядов

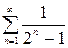1) ; 1а) ; 2) ; 2а) .

Решение. 1) Для сравнения выберем ряд , сходимость которого доказана. Так как имеет место очевидное неравенство , то данный ряд сходится.

1а) Выберем для сравнения тот же сходящийся ряд . Но неравенство  не позволяет сделать вывод о сходимости данного ряда – первая теорема сравнения не сработала.

2) Для сравнения выберем гармонический ряд , расходимость которого установлена. В силу неравенства  данный ряд расходится.

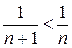2а) Выберем для сравнения тот же расходящийся ряд . Неравенство  не позволяет сделать вывод о расходимости данного ряда – опять первая теорема сравнения не сработала.

Примечание. Из утверждения 1 следует, что теорема справедлива и в случае, когда неравенство  выполняется, начиная с некоторого номера .

Следствие 1. Пусть  для всех  и пусть ряд  сходится. Тогда сходится и ряд .

Если же  для всех  и ряд  расходится, то расходится и ряд .

Следствие 2. Пусть  для всех  и пусть существует конечный предел , тогда ряды  и  ведут себя одинаково – сходятся или расходятся одновременно (т.е. не может быть так, что один из них сходится, а другой расходится).

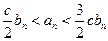Доказательство. . Выберем . Тогда  (т.к. )  при .

Если ряд  сходится, то сходится и ряд 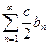 (по теореме). Но из следствия 1 получим, что и ряд  сходится.

Если ряд  сходится, то сходится и ряд , следовательно, сходится ряд

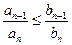Теорема (второй признак сравнения). Пусть  и  для всех  .

1. Если ряд  сходится, то сходится и ряд .

2. Если ряд  расходится, то расходится и ряд .

 

Пример. Исследовать сходимость рядов

1) ; 2) ; 3) .

Решение. 1) Для сравнения выберем сходящийся ряд 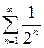. Так как (первый замечательный предел) , то оба ряда ведут себя одинаково – данный ряд сходится.

2) Опять для сравнения выберем сходящийся ряд 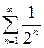. Так как , то оба ряда ведут себя одинаково – данный ряд сходится.

3) Для сравнения выберем расходящийся гармонический ряд . Так как , то оба ряда ведут себя одинаково – данный ряд расходится.

Признак Даламбера

Теорема (признак сходимости Даламбера). Пусть задан ряд с положительными членами  и при всех n: , где . Тогда ряд  сходится. Если же при всех n для этого ряда , то ряд расходится.

Доказательство. Пусть выполнено условие , . Рассмотрим вспомогательный ряд , сходящийся при . Тогда по второй теореме сравнения ряд  сходится, т.к. . Если же выполнено условие , то, взяв вспомогательный расходящийся ряд , по второй теореме сравнения получаем , значит, ряд  расходится.

В предельной форме этот признак выглядит так:

Теорема. Если существует , то при  ряд  сходится, а при  расходится. При  признак неприменим.

Доказательство. Пусть . Выбираем  так, чтобы и . Согласно определению предела последовательности найдется такой номер , что для всех  выполняется неравенство . По предыдущей теореме ряд сходится.

Если же , то выберем  так, чтобы . Тогда снова найдется такой номер , что для всех  выполняется неравенство  и ряд расходится.

Пример. Исследовать сходимость рядов

1) ; 2)   3)   4) .

Решение. 1) Воспользуемся признаком Даламбера в предельной форме. Выпишем -ый и –й члены ряда и составим отношение

.

Переходя к пределу при , получаем

.

В силу признака Даламбера ряд сходится.

2) Здесь .

Перейдем к пределу при . Вспоминая, что  (второй замечательный предел), получаем  – данный ряд сходится.

3) Здесь  – данный ряд расходится.

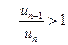4) Здесь , т.е. признак Даламбера в предельной форме не решает вопроса о поведении ряда. Более точная форма признака Даламбера (без перехода к пределу) позволяет установить расходимость данного ряда. Действительно, в отношении  знаменатель с ростом  монотонно возрастает, оставаясь меньше числа . Значит, отношение , а это означает расходимость данного ряда.