Свойства условно сходящихся рядов

Теорема Римана. Если знакопеременный ряд сходится условно, то изменяя порядок следования его членов, сумму ряда можно сделать равной любому наперед заданному числу (в том числе и сделать ряд расходящимся).

Сходимость знакочередующихся рядов можно установить с помощью признака Лейбница.

Теорема (признак Лейбница). Пусть для знакочередующегося ряда

выполнены условия:

1. ;

2. .

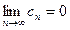Тогда этот ряд сходится и сумм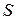а  ряда  удовлетворяет неравенству  

Доказательство. Рассмотрим частичную сумму ряда с номером : . Заметим, что

,

т.к. по условию 1 имеет место неравенство  для любого 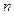. Значит, последовательность  не убывает.

Теперь конечное число слагаемых в сумме  сгруппируем иначе:

.

Все слагаемые в круглых скобках, а также  по условию 1 неотрицательны, значит, . Таким образом, последовательность  не убывает и ограничена сверху. Значит, существует предел . Кроме того, .

Осталось доказать, что . Имеем , но по условию 2 . Тогда . Теорема доказана.

Пример. Вернемся к ряду . Очевидно, что  и . По теореме Лейбница этот ряд сходится.

Приведем без доказательства еще один признак, применимый для любых рядов.

Теорема. (Признак Абеля-Дирихле). Если частичные суммы ряда  ограничены, а числа  образуют монотонную бесконечно малую последовательность, то ряд   сходится.

Пример. Исследовать сходимость ряда .

Решение. Здесь последовательность  монотонно стремится к нулю. Чтобы иметь право воспользоваться признаком Дирихле, докажем, что последовательность частичных сумм  ограничена. Подробно запишем цепочку преобразований -ой частичной суммы, начиная с введения вспомогательного множителя :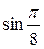

.

Здесь использованы тригонометрические соотношения

;

.

Теперь легко получить оценку:

.

Ограниченность частичных сумм доказана. В силу признака Дирихле данный знакопеременный ряд сходится.

Литература

1. Ильин В.А., Позняк Э.Г. Основы математического анализа: Учебник: В 2 т. - М.: Наука, 1982. - Т.I. - 616 с.; 1983. - Т.2. - 447 с.

2. 1. Кудрявцев Л.Д. Курс математического анализа: Учебник: В 2 т. - М.: Высш. шк., 1981. - Т. I. - 687 с.; 1981. - Т.2. - 584 с.

3. Никольский С.М. Курс математического анализа: Учебник: В 2 т. - М.: Наука, 1983. - Т. I. - 464 с., 1983. - Т.2. - 448 с.

4. Смирнов В.И. Курс высшей математики: Учебник: В 3 т. -М.: Наука, 1974. - Т.I. - Ч.I. - 323 с.; Т.3. - Ч.2 - 672 с.

5. Демидович Б.П. Сборник задач и упражнений по математическому анализу. - М.: Наука, 1979. - 527 с.

6. Берман Г.Н. Сборник задач и упражнений по математическому анализу. – М. Наука, 1969. – 430 с.