2020-06-08
192
ЛЕКЦИЯ 6
При доказательстве метода Якоби были получены выражения для канонических коэффициентов
.
Значит, если определители 
и 
имеют одинаковые знаки, то коэффициент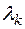 
положителен, если же их знаки различны, то 
. Поэтому число отрицательных канонических коэффициентов равно числу перемен знаков в последовательности чисел 
. Но мы уже обращали внимание на то, что можно было исходить из другого базиса (например, изменить порядок базисных векторов). Тогда исходная матрица была бы другой и другими были бы её главные миноры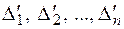 
. Заранее совершенно неясно, будет ли число перемен знака в обоих случаях одним и тем же.
Пусть квадратичная форма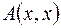 
, заданная в 
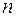-мерном линейном пространстве 
, в некотором базисе приведена к каноническому виду
.
Здесь 
- ранг квадратичной формы, не зависящий от выбора базиса. И пусть канонические коэффициенты 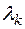занумерованы так, что первые 
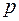из этих коэффициентов положительны, а остальные 
– отрицательны:
.
Рассмотрим невырожденное преобразование координат
В результате этого преобразования квадратичная форма принимает вид
,
называемый нормальным видом квадратичной формы. Здесь канонические коэффициенты равны +1 или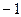 
(см. пример п. 39). Возникает вопрос, зависит ли количество коэффициентов, равных +1 или –1, от способа приведения квадратичной формы к нормальному виду.
Оказывается, имеет место теорема, которая называется законом инерции квадратичных форм.
Теорема. Число слагаемых с положительными (отрицательными) коэффициентами в нормальном виде квадратичной формы 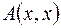не зависит от способа приведения формы к этому виду.
Доказательство. Пусть в базисе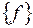 
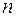-мерного линейного пространства вектор 
, а квадратичная форма имеет вид 
.
И пусть построены два канонических базиса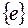 
и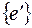 
. В базисе 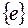вектор 
, а форма 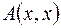имеет нормальный вид
, (1)
где 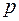положительных и 
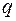отрицательных коэффициентов, 
(
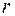- ранг формы). В базисе 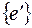вектор 
, а форма 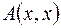имеет нормальный вид
, (2)
где 
положительных и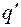 
отрицательных коэффициентов. Естественно, по прежнему 
. Достаточно показать, что 
.
Предположим, что это не так, т.е. 
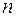. Убедимся, что тогда в -мерном пространстве существует ненулевой вектор 
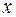, у удовлетворяющий условиям
1. В базисе 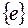первые 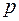координат вектор 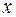равны нулю:
. (3)
2. В базисе 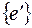равны нулю последние 
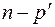координат вектора :
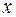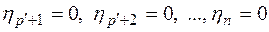. (4)
И координаты 
вектора 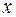в базисе 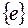, и координаты 
этого вектора в базисе 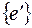линейно выражаются через его координаты 
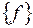в исходном базисе (п. 35). Поэтому уравнения (3) и (4) можно рассматривать как линейную однородную систему относительно 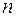неизвестных 
. А поскольку количество уравнений 
в силу предположения , то эта система имеет нетривиальное решение – вектор 
.
Подсчитаем значение квадратичной формы для такого вектора 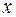. В соответствии с (1) и (3) в базисе 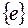получаем 
. С другой стороны, для этой же формы в базисе 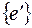(2) и (4) дают 
.
Очевидно, равенство
= 
+ =0
выполняется лишь при
и
. (5)
В силу (5) и (4) получаем, что в базисе 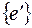вектор 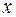имеет все координаты, равные нулю, т.е. 
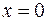. Тогда и в любом другом базисе, в частности, в исходном базисе 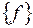координаты вектора 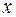должны быть равны нулю, но мы доказали, что . К противоречию привело предположение . По аналогичным соображениям ведет к противоречию и предположение 
. Итак, .¨
