2020-06-08
922
приведенных к нормальному виду
Пусть в некотором каноническом базисе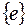 
квадратичная форма 
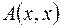приведена к нормальному виду (1). Полное число 
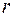членов, входящих в (1), т.е. ранг формы, называется также индексом инерции квадратичной формы; число 
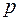положительных слагаемых называется положительным индексом инерции, а число 
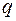отрицательных слагаемых - отрицательным индексом инерции. Напоминаем, что 
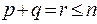.По нормальному виду квадратичной формы легко сделать вывод о ее знакоопределенности. Сформулируем и докажем несколько простых утверждений.
Критерий 1. Для того чтобы квадратичная форма 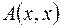, заданная в 
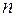-мерном линейном пространстве, была положительно (отрицательно) определена, необходимо и достаточно, чтобы её положительный (отрицательный) индекс инерции совпадал с размерностью пространства.
Доказательство провеём для положительно определённых форм, т.е. докажем
.
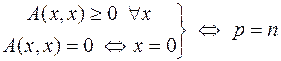Необходимость. Пусть форма 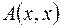положительно определена, тогда её нормальный вид содержит лишь положительные квадраты:
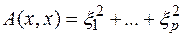6)
При этом если бы было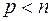 
, то форма (6) для некоторого вектора 
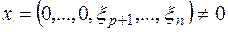была бы равна нулю, что противоречит её положительной определённости. Значит, 
.
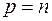Достаточность. Пусть 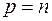, т.е. форма имеет вид
.
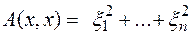Очевидно,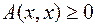 
для любого 
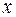, а равенство 
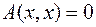возможно лишь при одновременном выполнении 
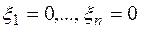, т.е. когда вектор 
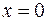. Значит, форма 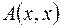в каждой точке пространства, кроме начала координат, принимает положительные значения, т.е. является положительно определённой.¨
Критерий 2. Для того чтобы квадратичная форма 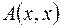, заданная в 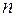-мерном линейном пространстве, была знакопеременной, необходимо и достаточно, чтобы как положительный, так и отрицательный её индексы инерции были отличны от нуля.
Докажем
.
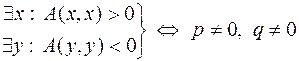Необходимость. Пусть форма 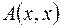является знакопеременной. Тогда в её нормальном виде (1) должны содержаться как положительные, так и отрицательные слагаемые, т.е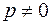. и 
, и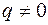 
.
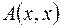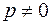Достаточность. Пусть у формы и , и 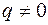. Тогда для некоторого вектора 
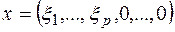форма принимает значение 
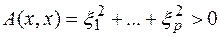, а для вектора 
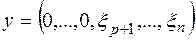соответственно 
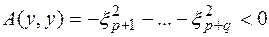. Значит, эта форма знакопеременна.¨
Критерий 3. Для того чтобы квадратичная форма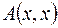 
, заданная в 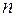-мерном линейном пространстве, была квазиположительно (квазиотрицательно) определённой, необходимо и достаточно, чтобы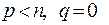 
.
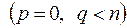Доказательство проведём для квазиположительно определённой формы:
.
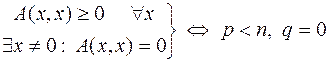Необходимость. Пусть форма 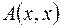квазиположительно определена, тогда, очевидно, в представлении (1) должны отсутствовать отрицательные слагаемые, т.е. 
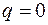. Кроме того, должно быть 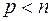, ибо при 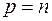форма была бы положительно определённой.
Достаточность. Пусть 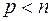и 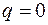, тогда
,
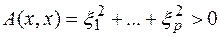но для некоторого ненулевого вектора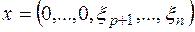 
имеем 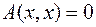, а такая форма квазиположительно определена.¨
Критерий Сильвестра позволяет выяснить вопрос о знакоопределённости квадратичной формы, заданной в произвольном базисе, без приведения её к каноническому виду.
Пусть в некотором базисе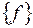 
форма 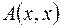определена своей матрицей 
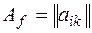, т.е. 
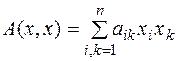, и пусть 
, 
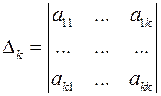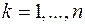
- угловые миноры этой матрицы. Имеет место следующая
Теорема (критерий Сильвестра).
1. Для того чтобы квадратичная форма 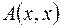была положительно определённой, необходимо и достаточно, чтобы все угловые миноры были положительными:
.
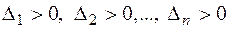2. Для того чтобы квадратичная форма 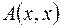была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров чередовались, начиная с 
.
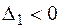Докажем первую часть критерия, опираясь на теорему Якоби (п. 40).
Необходимость. Пусть форма 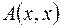положительно определена. Докажем сначала, что тогда все угловые миноры матрицы 
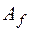отличны от нуля. Предположим противное: пусть форма положительно определена, но 
.
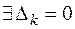Рассмотрим вспомогательную квадратную однородную систему:
.
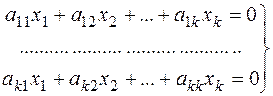Так как определитель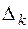 
этой системы по предположению равен нулю, то система нетривиально совместна, т. е. имеет решение 
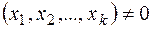. Построим на этой системе отрезок квадратичной формы, умножая обе части первого уравнения на 
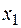, второго – на 
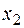,…, последнего – на 
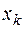и складывая их:
.
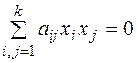Прибавим к левой части сумму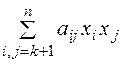 
, которая равна нулю, если взять 
… 
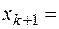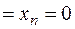. Рассмотрим вектор 
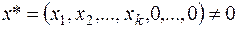. Запишем для него квадратичную форму 
:
+ 
.
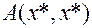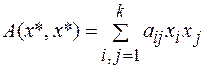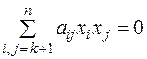
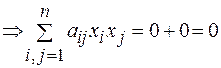Получили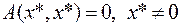 
, а это противоречит условию положительной определённости заданной формы.
Значит, ни один из угловых миноров положительно определённой квадратичной формы не может равняться нулю. Но при условии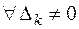 
по теореме Якоби форма 
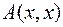приводится к каноническому виду
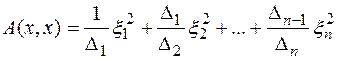. (7)
Так как у положительно определённой квадратичной формы все канонические коэффициенты положительны, получаем:
.
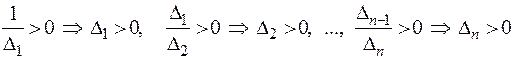Достаточность. Пусть все угловые миноры положительны. Тогда они не равны нулю и в силу теоремы Якоби имеет место представление (7), где все канонические коэффициенты положительны,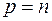 
. В силу критерия 1 предыдущего пункта это и означает, что форма положительно определена. ¨
Доказательство второй части критерия Сильвестра для отрицательно определённых квадратичных форм предлагаем провести самостоятельно.
Пример. Покажем, как работает критерий Сильвестра при проверке достаточных условий экстремума функции двух переменных. Рассмотрим функцию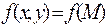 
, дифференцируемую в некоторой окрестности точки 
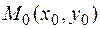и дважды дифференцируемую в самой точке 
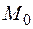. Пусть 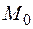- стационарная точка, т.е. выполняются необходимые условия экстремума
.
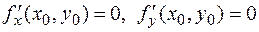Мы знаем, что в стационарной точке не гарантировано наличие экстремума. Возникает вопрос об условиях, достаточных для существования (или отсутствия) экстремума. Иначе, стационарную точку следует подвергнуть дополнительному исследованию.
Естественно обратиться к рассмотрению разности
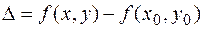
и вспомнить, что если для всех точек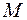 
из некоторой окрестности точки 
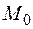имеет место неравенство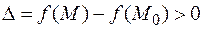 
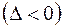, то в точке 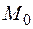функция 
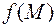имеет локальный минимум (максимум).
Разложим разность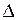 
по формуле Тейлора, ограничиваясь двумя членами (впрочем, первый член исчезает, так как точка 
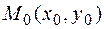- стационарная):
.
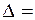
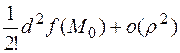Здесь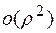 
- остаточный член в форме Пеано, 
, 
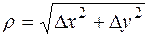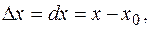
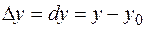. Очевидно, знак 
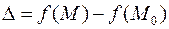–приращения функции 
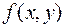в стационарной точке 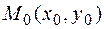– совпадает со знаком второго дифференциала функции в этой точке: 
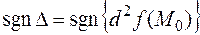. Но второй дифференциал представляет собой квадратичную форму относительно переменных 
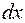и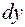 
:
.
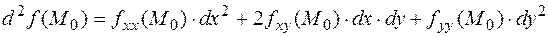Запишем матрицу этой квадратичной формы:
.
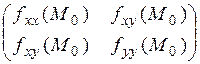Исследуем знакоопределенность формы с помощью критерия Сильвестра. Если угловые миноры
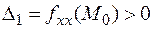и 
,
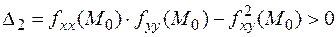то квадратичная форма положительно определена, т.е. второй дифференциал (а с ним и приращение 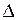) сохраняет положительный знак в некоторой окрестности точки 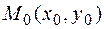. Тогда это точка локального минимума функции .
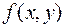Если знаки угловых миноров чередуются, так что
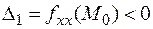и 
,
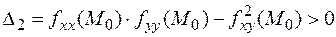то квадратичная форма отрицательно определена, т.е. второй дифференциал (а с ним и приращение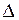 
) сохраняет отрицательный знак в некоторой окрестности точки 
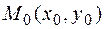. Тогда 
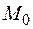– точка локального максимума функции .
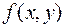Наконец, если определитель матрицы меньше нуля:
,
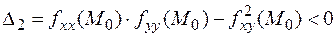то в силу критерия Сильвестра не может быть и речи о знакоопределённости квадратичной формы. В этом случае в стационарной точке 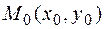функция 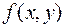экстремума не имеет.
Легко проверить, что функция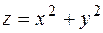 
(параболоид вращения) в стационарной точке 
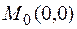имеет минимум, а функция 
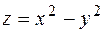(гиперболический параболоид) в этой точке не имеет экстремума.♦
