Собственные векторы и собственные значения
Линейного оператора
Пусть 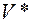 - некоторое подпространство пространства
- некоторое подпространство пространства 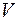 и
и 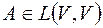 . Вообще говоря, для произвольного
. Вообще говоря, для произвольного 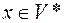 вектор
вектор 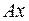 не обязательно принадлежит
не обязательно принадлежит 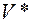 . Однако может случиться, что некоторые подпространства переходят сами в себя под действием оператора
. Однако может случиться, что некоторые подпространства переходят сами в себя под действием оператора 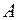 .
.
Определение. Линейное подпространство 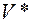 называется инвариантным относительно оператора
называется инвариантным относительно оператора 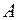 , если
, если 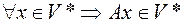 .
.
Тривиальными инвариантными подпространствами является все пространство, а также подпространство, состоящее только из нуль-вектора.
Примеры. 1. Пусть в 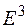 задан оператор поворота на некоторый угол вокруг оси
задан оператор поворота на некоторый угол вокруг оси 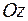 . Инвариантными подпространствами являются, во-первых, ось вращения (одномерное инвариантное подпространство), во-вторых, плоскость
. Инвариантными подпространствами являются, во-первых, ось вращения (одномерное инвариантное подпространство), во-вторых, плоскость 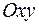 , ортогональная оси вращения (двумерное инвариантное подпространство).
, ортогональная оси вращения (двумерное инвариантное подпространство).
2. На плоскости 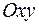 задан оператор, растягивающий плоскость в
задан оператор, растягивающий плоскость в 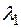 раз вдоль оси
раз вдоль оси 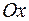 и в
и в 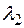 раз вдоль оси
раз вдоль оси 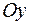 :
:
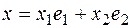
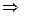
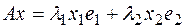 .
.
Координатные оси в этом случае - одномерные инвариантные подпространства. В частности, при 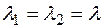 оператор
оператор 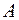 есть преобразование подобия с коэффициентом
есть преобразование подобия с коэффициентом 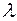 , а любая прямая, проходящая через начало координат, есть инвариантное подпространство.
, а любая прямая, проходящая через начало координат, есть инвариантное подпространство.
3. Рассмотрим в пространстве 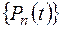 ,
, 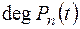
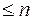 оператор дифференцирования:
оператор дифференцирования: 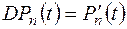 . Совокупность многочленов степени
. Совокупность многочленов степени 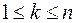 образует инвариантное подпространство. Действительно, дифференцируя многочлен степени
образует инвариантное подпространство. Действительно, дифференцируя многочлен степени 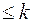 , мы получим многочлен, степень которого снова не превосходит
, мы получим многочлен, степень которого снова не превосходит 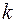 .
.
4. Ядро и образ линейного оператора 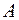 являются инвариантными подпространствами.
являются инвариантными подпространствами.
Особую роль в дальнейшем будут играть одномерные инвариантные подпространства.
Пусть 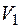 - одномерное подпространство, порожденное вектором
- одномерное подпространство, порожденное вектором 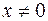 (совокупность векторов вида
(совокупность векторов вида 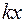 ). По определению, пространство
). По определению, пространство 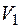 инвариантно относительно оператора
инвариантно относительно оператора 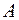 тогда и только тогда, если вектор
тогда и только тогда, если вектор 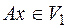 , т.е. вектор
, т.е. вектор 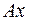 кратен вектору
кратен вектору 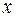 :
: 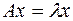 .
.
Определение. Вектор 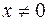 , удовлетворяющий соотношению
, удовлетворяющий соотношению 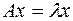 , называется собственным вектором, а соответствующее число
, называется собственным вектором, а соответствующее число 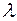 - собственным значением (характеристическим числом) оператора
- собственным значением (характеристическим числом) оператора 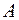 .
.
Итак, если 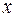 - собственный вектор, то векторы
- собственный вектор, то векторы 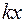 образуют одномерное инвариантное подпространство. И наоборот: все ненулевые векторы одномерного инвариантного подпространства являются собственными.
образуют одномерное инвариантное подпространство. И наоборот: все ненулевые векторы одномерного инвариантного подпространства являются собственными.
Имеет место следующая
Основная теорема. В комплексном линейном пространстве каждый линейный оператор 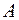 имеет хотя бы один собственный вектор.
имеет хотя бы один собственный вектор.
Доказательство. Пусть 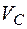 - комплексное
- комплексное 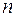 -мерное линейное пространство и
-мерное линейное пространство и 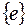 - произвольный базис в этом пространстве. И пусть оператор
- произвольный базис в этом пространстве. И пусть оператор 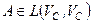 определяется в этом базисе матрицей
определяется в этом базисе матрицей 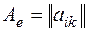 . Тогда
. Тогда 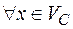 представляется в виде
представляется в виде
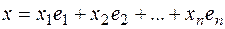 ,
,
а вектор 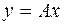 - в виде
- в виде
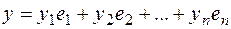 ,
,
Пусть вектор 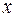 - собственный для оператора
- собственный для оператора 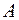 , т.е.
, т.е. 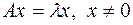 . В матричной записи это выглядит так:
. В матричной записи это выглядит так:
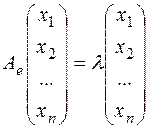 или
или 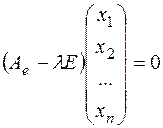 .
.
Перепишем последнее условие в координатной форме:
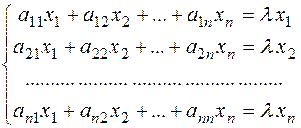
Иначе:
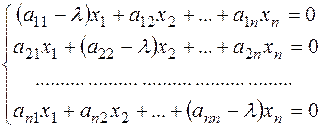 (1)
(1)
Нам надо доказать, что система (1) имеет нетривиальное решение 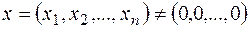 . Критерием нетривиальной совместности квадратной системы является равенство нулю ее определителя:
. Критерием нетривиальной совместности квадратной системы является равенство нулю ее определителя:
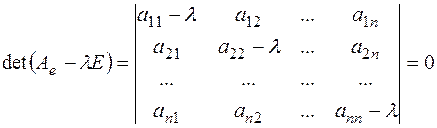 . (2)
. (2)
Получили уравнение 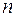 -ой степени относительно
-ой степени относительно 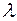 , которое в поле комплексных чисел имеет хотя бы один корень
, которое в поле комплексных чисел имеет хотя бы один корень 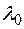 (основная теорема алгебры). Подставляя в систему (1) этот корень, найдем ненулевое решение системы
(основная теорема алгебры). Подставляя в систему (1) этот корень, найдем ненулевое решение системы 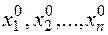 . Тогда вектор
. Тогда вектор 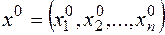 будет собственным вектором, а число
будет собственным вектором, а число 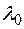 - собственным значением оператора
- собственным значением оператора 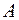 :
: 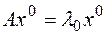 .¨
.¨
Замечание. Доказательство теоремы остается в силе, если рассматривать оператор 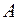 не во всем пространстве
не во всем пространстве 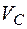 , а в любом его инвариантном подпространстве. Поэтому в любом инвариантном подпространстве существует хотя бы один собственный вектор оператора
, а в любом его инвариантном подпространстве. Поэтому в любом инвариантном подпространстве существует хотя бы один собственный вектор оператора 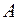 .
.
Определение. Многочлен 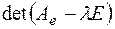 , стоящий в левой части уравнения (2), называется характеристическим многочленом оператора
, стоящий в левой части уравнения (2), называется характеристическим многочленом оператора 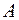 , а само уравнение (2) - характеристическим (вековым) уравнением.
, а само уравнение (2) - характеристическим (вековым) уравнением.
Следствие. Число 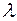 является собственным значением оператора
является собственным значением оператора 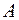 тогда и только тогда, когда это число – корень характеристического уравнения.
тогда и только тогда, когда это число – корень характеристического уравнения.
При переходе к другому базису матрица оператора 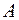 (и оператора
(и оператора 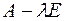 ) изменяется, но eё определитель остается неизменным. Поэтому будем обозначать характеристический многочлен
) изменяется, но eё определитель остается неизменным. Поэтому будем обозначать характеристический многочлен 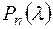 =
=  , подразумевая под матрицей
, подразумевая под матрицей 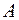 матрицу линейного оператора
матрицу линейного оператора 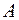 в произвольном базисе. Теперь характеристическое уравнение кратко запишем так:
в произвольном базисе. Теперь характеристическое уравнение кратко запишем так:
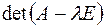 =0.
=0.
Представим характеристический многочлен в виде
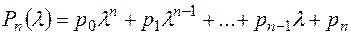 .
.
Коэффициенты 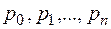 , построенные по матрице
, построенные по матрице 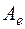 оператора
оператора 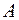 , не зависят от выбора базиса, так как этим свойством обладает характеристический многочлен. Можно выразить
, не зависят от выбора базиса, так как этим свойством обладает характеристический многочлен. Можно выразить 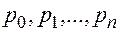 явно через элементы матрицы
явно через элементы матрицы 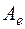 . Очевидно, старший коэффициент
. Очевидно, старший коэффициент 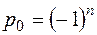 . Мы обратим внимание на коэффициенты
. Мы обратим внимание на коэффициенты 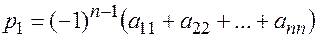 и
и 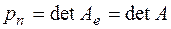 , играющие наибольшую роль. Эти коэффициенты в силу теоремы Виета с точностью до знака совпадают:
, играющие наибольшую роль. Эти коэффициенты в силу теоремы Виета с точностью до знака совпадают: 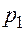 – с суммой, а
– с суммой, а 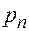 – с произведением всех корней характеристического уравнения (всех собственных значений). Сумма
– с произведением всех корней характеристического уравнения (всех собственных значений). Сумма 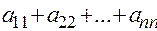 называется следом матрицы
называется следом матрицы 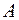 и обозначается
и обозначается 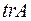 (от английского trace - след) или
(от английского trace - след) или 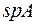 (от немецкого spur).
(от немецкого spur).
В заключение обратим внимание на одно важное свойство характеристического многочлена.
Теорема Гамильтона-Кэли. Если 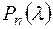 - характеристический многочлен матрицы
- характеристический многочлен матрицы 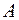 , то
, то 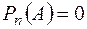 . Иначе: всякая матрица обнуляет свой характеристический многочлен.
. Иначе: всякая матрица обнуляет свой характеристический многочлен.
Пример. Для матрицы 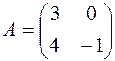 найдём собственные значения и собственные векторы.
найдём собственные значения и собственные векторы.
Собственный вектор 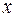 матрицы (оператора)
матрицы (оператора) 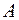 определяется условием
определяется условием
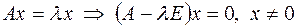 .
.
Значит, координаты 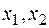 собственного вектора находятся как нетривиальное решение однородной линейной системы
собственного вектора находятся как нетривиальное решение однородной линейной системы
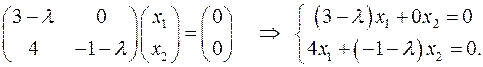 (*)
(*)
Составим характеристическое уравнение 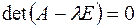 :
:
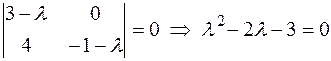 . (**)
. (**)
Корни этого уравнения - собственные значения - 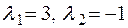 .
.
Найдём собственный вектор 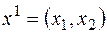 , соответствующий собственному значению
, соответствующий собственному значению 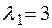 .
.
Поставим в систему (*) 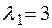 :
:
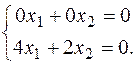
Отсюда находим 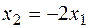 (одна свободная неизвестная). Полагая, например,
(одна свободная неизвестная). Полагая, например, 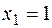 , получим
, получим 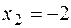 . Первый собственный вектор с точностью до постоянного множителя определён:
. Первый собственный вектор с точностью до постоянного множителя определён: 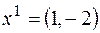 .
.
Найдём второй собственный вектор 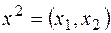 , соответствующий собственному значению
, соответствующий собственному значению 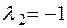 . Поставим в систему (*)
. Поставим в систему (*) 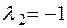 :
:
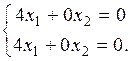
Отсюда находим 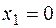 ,
, 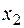 произвольно (свободная неизвестная). Полагая, например,
произвольно (свободная неизвестная). Полагая, например, 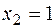 , получим второй собственный вектор с точностью до постоянного множителя:
, получим второй собственный вектор с точностью до постоянного множителя: 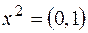 .
.
Легко проверить, что найденные собственные векторы линейно независимы.
Убедимся, что данная матрица удовлетворяет своему характеристическому уравнению. Для этого надо подставить матрицу 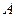 в левую часть уравнения (**):
в левую часть уравнения (**):
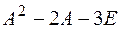 .
.
Вычислим 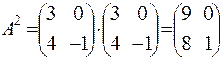 ,
, 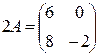 ,
, 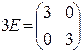 .
.
Теперь 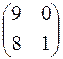
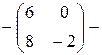
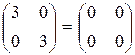 , как и должно быть в силу теоремы Гамильтона-Кэли.
, как и должно быть в силу теоремы Гамильтона-Кэли.
 2020-06-08
2020-06-08 1754
1754