В комплексном пространстве

Определение. Числовая функция  векторного аргумента 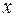, определённая в комплексном линейном пространстве , называется линейной формой (линейной функцией) первого рода, если  она ставит в соответствие комплексное число , причём выполняются следующие условия:

1° ,

                            2°

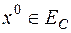Это совпадает с определением линейной формы в вещественном пространстве. Например, при  и некотором фиксированном  функция  представляет собой линейную форму первого рода.

Определение. Числовая функция  векторного аргумента 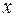, определённая в комплексном линейном пространстве , называется линейной формой второго рода, если  она ставит в соответствие комплексное число , причём выполняются следующие условия:

1° ,

                            2°

       Здесь  - комплексное число, сопряженное с числом . Например, при  и некотором фиксированном 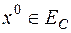 функция  представляет собой линейную форму второго рода.

Можно показать, что всякая линейная форма первого рода может быть записана в виде

,

где  - координаты вектора  в базисе , а числа .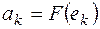

Всякая линейная форма второго рода может быть записана в виде

.

Очевидно, если  есть линейная форма первого рода, то  - линейная форма второго рода.

       Так как билинейная форма  есть функция двух векторов, линейная по каждому из аргументов, то наличие в комплексном пространстве двух типов линейных функций приводит к существованию четырех типов билинейных форм. Нас интересуют только те билинейные формы, у которых линейность по аргументу  первого рода, а по аргументу  - второго рода.

Определение. Числовая функция  от двух векторных аргументов 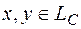 называется билинейной формой, если  она ставит в соответствие комплексное число 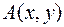, причём для любого комплексного числа  выполняются следующие условия:

1°.

2°. .

.      Примером билинейной формы в комплексном пространстве является скалярное произведение в комплексном евклидовом пространстве 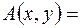, рассматриваемое как функция векторов  и . Легко проверить, что условия, определяющие билинейную форму, в этом случае выполнены.

       Пусть в -мерном комплексном пространстве задан базис  и определена билинейная форма  как функция векторов  и .

Тогда из определения билинейной формы следует:

.

Матрица  из чисел  называется  матрицей билинейной формы  в базисе .

Определение. Билинейная форма называется эрмитовой, если

= .

Это понятие является аналогом симметричной билинейной формы в вещественном пространстве. Например, билинейная форма 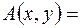, определенная как скалярное произведение в комплексном евклидовом пространстве, является эрмитовой, т.к. выполнено условие . А скалярное произведение в вещественном евклидовом пространстве – симметричная билинейная форма.

Для того чтобы форма  была эрмитовой, необходимо и достаточно, чтобы ее матрица в каком либо базисе удовлетворяла условию 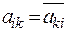. Действительно, если форма  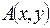эрмитова, то . Обратно, если , то .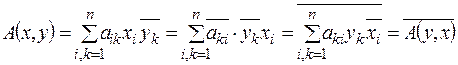

Очевидно, если для матрицы формы  условие  выполняется в каком либо базисе, то оно выполнено и в любом другом базисе. В самом деле, 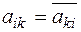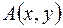= , но тогда и в любом другом базисе .

       Так же, как это было сделано для вещественного пространства, можно показать, что если  и 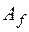 - матрицы билинейной формы  в базисах  и  соответственно, то . Здесь 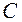 - матрица перехода от базиса  к базису , а - матрица, транспонированная и комплексно-сопряженная к матрице  (напоминаем, что в аналогичной формуле для вещественного пространства вместо  фигурировала матрица ).

Если в эрмитовой билинейной форме  положить , то получим эрмитову квадратичную форму. Примером эрмитовой квадратичной формы является скалярный квадрат

.

       В комплексном пространстве справедливы теоремы о приведении квадратичной формы к сумме квадратов, а также закон инерции и критерий положительной определенности квадратичной формы.