1. В университетскую библиотеку привезли новые учебники для четырех курсов, по 70 штук для каждого курса. В книжном шкафу 7 полок, на каждой полке помещается 25 учебников. Какое наименьшее количество шкафов потребуется, чтобы в них разместить все новые учебники?
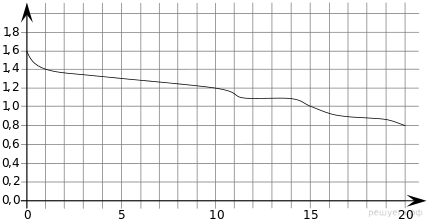
2. При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, за сколько часов напряжение упадёт с 1,4 вольта до 1 вольта.
3. 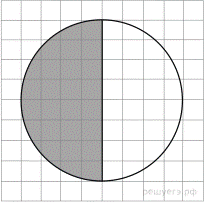 На клетчатой бумаге с размером клетки
На клетчатой бумаге с размером клетки 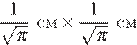 изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
4. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
5. Найдите корень уравнения: 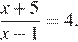
6. 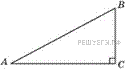 Один острый угол прямоугольного треугольника на 38° больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Один острый угол прямоугольного треугольника на 38° больше другого. Найдите больший острый угол. Ответ дайте в градусах.
7. 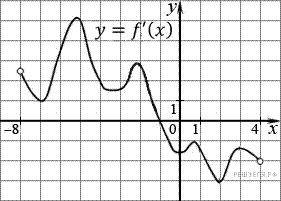 На рисунке изображен график производной функции f (x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f (x) принимает наименьшее значение?
На рисунке изображен график производной функции f (x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f (x) принимает наименьшее значение?
8. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
9. Найдите значение выражения 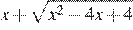 при
при 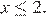
10. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону 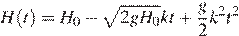 , где
, где 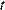 — время в секундах, прошедшее с момента открытия крана,
— время в секундах, прошедшее с момента открытия крана, 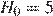 м — начальная высота столба воды,
м — начальная высота столба воды, 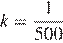 — отношение площадей поперечных сечений крана и бака, а
— отношение площадей поперечных сечений крана и бака, а 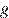 — ускорение свободного падения (считайте
— ускорение свободного падения (считайте 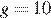 м/с
м/с 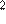 ). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?
). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?
11. В 2008 году в городском квартале проживало 40 000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 3%, а в 2010 году — на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
12. Найдите точку максимума функции 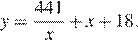
 2020-06-08
2020-06-08 117
117







