Изучения свойств арифметических действий в младших и старших классах

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ                                        РОССИЙСКОЙ  ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное

Учреждение высшего образования

 ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

         Факультет физико-математических и естественных наук

Кафедра «Математическое образование»

Контрольная работ по дисциплине «Методика обучение и воспитание (математика)»

        

Направление подготовки -44.03.01 Педагогическое образование.

Профиль подготовки- Maтематика

                                                           

                                                             Выполнил студент:___________ _Розметов А.

                                                                                    (ФИО)

                                                                                           Группа: 17ЗФПМ51

                                              Руководитель: доцент: _____________ Марина Е.В.

                                Работа защищена с оценкой _____________

                                     Преподаватели                ______________

                                                                                   ______________

                                     Дата защиты                   ______________

                                                                                                               

Пенза, 2020 г.

Содержание.

 

1.Индукция и дедукция.

2.Индукция и ее виды.

3.Дедукция и ее виды.

4.Метод математической индукции.

Изучения свойств арифметических действий в младших и старших классах.

Свойства степени в 7 классе.

Работа над понятием ТРАПЕЦИИ

Технологическая карта урока.

Список использованных источников.

1.Индукция и дедукция.

Определение индукции и дедукции.

Различают два вида рассуждений: индукцию и дедукцию.

Дедукция (от лат. deduction – выведение) или дедуктивный метод – способ рассуждения от общего к частному, от общих положений к частным заключениям. Например, применение любого из признаков делимости.

Простыми словами, Дедукция – это вариант мышления, при котором человек делает определенные логические выводы, основываясь на знаниях о классе вещей в целом, и переносит определенные черты на конкретную вещь. Другими словами, можно сказать что дедукция, это вариант логических рассуждений, направленных от общего к частному.

Несмотря на витиеватость определения, само понятие дедукции является весьма простым, особенно если понимать принцип работы дедуктивного метода. Итак, Дедуктивный метод работает следующим образом: Если мы знаем, что все представители определенного класса обладают каким-то свойством, то при рассмотрении одного из представителей этого класса, справедливо будет предположить, что и он обладает этим свойством. Так к примеру: Если мы знаем, что все люди смертны, а гипотетический Сережа — человек, то, следовательно, он тоже смертен.

Пример ДЕДУКЦИИ

У всех птиц есть перья. Попугай – это птица, следовательно, у попугая есть перья;

§ В красном мясе содержится железо. Говядина — красное мясо, поэтому в говядине есть железо;

§ Рептилии – холоднокровные, а змеи, это рептилии. Следовательно, змеи – холоднокровные;

§ Если A = B и B = C, то A = C;

Индукция -(от лат. induction – наведение) – способ рассуждения от частного к общему, от фактов к обобщениям. Например, установление признаков делимости на 10, 5, 3 и 2 в VI классе (индукция используется при выводе признаков: признаки делимости устанавливаются, исходя из наблюдения за таблицей умножения).

Индукция и дедукция не изолированы друг от друга, а находятся в диалектическом единстве. Всякая научная дедукция является результатом предварительного индуктивного изучения материала и применением индуктивно полученных результатов.

Что такое ИНДУКЦИЯ – простыми словами — это метод построения логического умозаключения основанный на принципе: от частного к общему. Так к примеру, если мы видим, что гипотетический Сережа умер, и он является человеком, то можно предположить, что все люди смертны.

Подведя итог, можно сказать что:
Индуктивные и дедуктивные рассуждения — это два противоположных, но не исключающих друг друга подхода, которые можно использовать для оценки выводов. Дедуктивное рассуждение предполагает наличие общего утверждения, из которого в дальнейшем и строится вывод о частном случае. С другой стороны, индуктивное рассуждение берет за основу серию частных случаев из которых и формируется общая теория. Подходы имеют различия, но важно понимать, что как индуктивное, так и дедуктивное рассуждение может оказаться ложным особенно если исходная предпосылка аргументации неверна. Оптимальным вариантом при построении логических выводов является использование комбинации этих методов.

Так к примеру, если мы видим, что гипотетический Сережа умер, и он является человеком, то можно предположить, что все люди смертны.

На заметку: Шерлок Холмс (литературный персонаж, созданный Артуром Конан Дойлом) – не использовал только дедуктивный метод. В большинстве случаев он строил свои выводы используя модель индуктивных рассуждений.

2.Индукция и ее виды.

Индуктивное умозаключение сложилось в процессе многовековой общественно-исторической и производственной практики и обязано своим происхождением наблюдению и опыту. Как разновидность вывода, индукция упомянута впервые в трудах древнегреческого философа Сократа (469 – 399 гг. до н. э.)

Термин «индукция» имеет три основных значения:

1) это один из видов рассуждений, при котором из двух или нескольких единичных (это S есть р) или частных (некоторое S есть p) высказываний получают новое общее высказывание (все S есть р).

2) это метод исследования, при котором желая изучить некоторое множество объектов (некоторых явлений), изучают отдельные объемы (обстоятельства), устанавливая в них те свойства, которые присущи всему рассматриваемому множеству объектов (или те обстоятельства, от которых зависит данное явление);

3) это форма изложения (беседа, процесс обучения), когда от менее общих положений приходят к общим положениям (заключениям, выводам).

Рассмотрим следующие примеры:

Пример 1. Единичные суждения: если дискриминант D квадратного уравнения с действительными коэффициентами больше нуля, то квадратное уравнение имеет два действительных корня; если D=0, то уравнение имеет один действительный корень; если D<0, то квадратное уравнение не имеет действительных корней.

Частное суждение: D>0, D=0, D<0 исчерпывают все случаи, которые могут быть относительно дискриминанта.

Новое общее суждение: всякое квадратное уравнение с действительными коэффициентами имеет не более двух действительных корней.

Здесь индукция выступает как особая форма вывода (умозаключения).

Пример 2.

Рассмотрим последовательность, заданную формулой

.

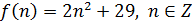Опытным путем находим, что

f(0)=29, f(1)=31, f(2)=37.

Наблюдение и вывод: последовательность 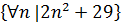является последовательностью простых чисел (ложное высказывание, так как

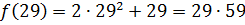– составное число).

– составное число).

Здесь индукция выступает как метод научного исследования, основанный на наблюдении и опыте.

В истории математики были случаи, когда известные математики ошибались в своих индуктивных выводах. Например, П. Ферма предположил, что все числа вида 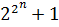простые, исходя из того, что при

m = 1, 2, 3, 4 они являются таковыми, но Л. Эйлер нашел, что уже при m = 5 число 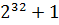не является простым (оно делится на 641).

Однако возможность получения с помощью индукции ложного заключения не является основанием для отрицания роли индукции в школьном обучении математике. Во-первых, применение индукции в учении корректируется и направляется учителем к открытию истин. Во-вторых, нужно добиваться понимания учащимися правдоподобного характера индуктивного заключения. Поэтому, применяя индукцию, необходимо всячески подчеркивать, что заключение является лишь предположением, гипотезой, которое может быть доказано (если оно истинно) или опровергнуто (если оно ложно).

Пример 3.

Знакомя учащихся с высотой треугольника, учитель чертит на доске треугольники разных видов и в каждом из них ученики проводят по три высоты; из рассмотрения этих чертежей учащиеся приходят к выводу, что три высоты в остроугольном и прямоугольном треугольниках пересекаются в одной точке (она лежит внутри треугольника или совпадает с вершиной). А в тупоугольном треугольнике проходят через одну точку прямые, которым принадлежат высоты. Здесь индукция выступает в роли метода обучения.

Различают два основных вида индукции: неполную и полную. Неполная индукция (как метод исследования) – индукция, при которой не исчерпываются все частные случаи, относящиеся к данной ситуации.

Как отмечает Д. Пойа [3, с. 111], Л. Эйлер – мастер индуктивного исследования в математике, он сделал важные открытия с помощью индукции (о бесконечных рядах, в теории чисел и др. областях), т.е. с помощью наблюдения, дерзкой догадки и проницательных подтверждений. Однако Л. Эйлер в этом отношении не является единственным: другие математики, известные и менее известные, в своей работе также пользуются индукцией. Все же в одном отношении Л. Эйлер кажется почти единственным: он старается изложить относящиеся к вопросу индуктивные доводы заботливо, в деталях, в хорошем порядке. Он излагает их убедительно, но честно, как это подобает настоящему ученому. Его изложение является чистосердечным изложением идей, приведших его к этим открытиям, и имеет особую прелесть.

С точки зрения логики, неполной индукцией называется вывод, основанный на рассмотрении одного или нескольких (но не всех) единичных или частных суждений, относящихся к рассматриваемому понятию (или системе понятий). Например, законы арифметических действий в школе (переместительный, сочетательный и т.д.) изучаются с помощью неполной индукции.

Вывод, основанный на неполной индукции, может быть ошибочным, поэтому индукция в качестве метода исследования применяется весьма осторожно. Значение неполной индукции состоит в том, что рассмотрение частных случаев позволяет выявить закономерность, помогает высказать гипотезу о характере этой закономерности; доказательство же должно быть осуществлено другим путем (обычно дедукцией). Неполная индукция позволяет догадаться об идее доказательства перед тем, как проведете его в деталях.

В процессе обучения школьников к неполной индукции нужно относиться осторожно, учащиеся должны знать, что заключения по индукции могут быть и ложными, и истинными, они нуждаются в доказательстве. Но пренебрегать неполной индукцией нельзя, в этом методе реализуется принцип обучения «от простого к сложному», изучение новых абстрактных понятий и высказываний проходит естественным путем через опыт и наблюдение, через восприятие и представление и т.д. Кроме того, используя индуктивный метод обучения, мы обучаем учащихся математической деятельности, «наводим» самих учащихся на новое понятие, теорему или формулу. Но вывод надо делать на рассмотрении не одного, а нескольких частных случаев.

Полной индукцией называется вывод, основанный на рассмотрении всех единичных или частных суждений (случаев), относящихся к рассматриваемой ситуации. Если число этих случаев конечно и все они рассмотрены, то вывод, сделанный путем полной индукции, можно считать обоснованным.

Например, теорема об измерении вписанного угла, теорема косинусов.

Пример 4. В треугольнике ABC проведена высота СD. Какая из трех точек А, B и D лежит между двумя другими, если углы А и В треугольника острые. (Решение: точка В не может лежать между А и D, если бы она лежала между ними, то угол АВС был бы равен сумме углов ВСD и СDВ по теореме о внешнем угле треугольника, а значит острый угол В (по условию) был бы больше прямого. Точно так же точка А не может лежать между точками В и D. Значит, точка D лежит между точками А и В).

3.Дедукция и ее виды.

Дедукция есть форма вывода, при которой из одного общего или одного частного высказывания получают новое, менее общее или частное суждение. Дедуктивные процессы на строгом уровне описываются в исчислениях математической логики, а впервые теорию дедукции разработал Аристотель. Р. Декарт считал, что к познанию вещей человек приходит двумя путями: через опыт и с помощью дедукции, которую он называл умозаключением; опыт часто вводит нас в заблуждение, а дедукция избавляет нас от этого недостатка.

Дедуктивные выводы могут быть представлены следующими видами:

· Переход от более общего положения к менее общему или единичному.

Пример 5.

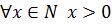
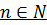
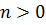
· Переход от более общего положения к общему положению, ему подчиненному.

Пример 6.

Сумма углов треугольника равна 180°, значит, сумма углов прямоугольного треугольника также равна 180°, поэтому сумма острых углов прямоугольного треугольника равна 90°.

· Переход утверждения одной общности к утверждению той же общности.

Пример 7. Область определения четной (нечетной) функции симметрична относительно точки 0. Множество всех точек, соответствующих натуральным числам, не симметрично относительно никакой точки. Вывод: никакая функция с областью определения N не является четной (нечетной).

· Переход от единичного положения к частному.

Пример 8.

Число е – трансцендентное.

Число π – трансцендентное.

Некоторые иррациональные числа трансцендентны.

Математика является дедуктивной наукой. При строгом изложении любой математической дисциплины устанавливается система основных понятий и отношений (которые не определяются), затем конструируется система аксиом, связывающая эти понятия и отношения. На основе системы основных понятий, отношений и аксиом образуются новые понятия (которые определяются через известные понятия и отношения), и посредством правил вывода строятся новые теоремы и следствия из них, излагаемые в логической последовательности. Дедуктивное доказательство теорем характеризуется не только логической последовательностью шагов, но и обязательностью обоснования каждого шага ссылками на известные математические предложения, предшествующие рассматриваемым.

Как метод исследования дедукция характеризуется тем, что для получения нового знания о некотором объекте (понятии, свойстве) находят ближайший к данному объекту класс объектов (ближайшее родовое понятие) и применяют к этому объекту (понятию) существенные свойства этого класса объектов (признаки рода).

Например, изучая свойства прямоугольника, мы устанавливаем, что он есть параллелограмм, поэтому обладает всеми свойствами параллелограмма.

Дедукция может выступать в виде особой формы изложения материала в учебнике, как один из методов обучения, при котором от общих правил и положений приходят к менее общим или частным правилам или положениям. Например, применяя признаки подобия треугольника к рассмотрению конкретных задач, мы используем дедукцию.

В процессе развития математики индукция и дедукция не выступают изолированно: они тесно переплетаются между собой, часто бывают просто неразличимы. (Выводя из наблюдений признак делимости на 2, учащиеся пользуются индукцией, применяя его – дедукцией).

4.Метод математической индукции.

 

Особенно ярко взаимосвязь индукции и дедукции выступает при изучении математических предложений, доказываемых методом математической индукции.

Например, при выводе формулы бинома Ньютона.

1) Наблюдение и опыт:

(a + b)⁰ = 1

(a + b)¹ = a + b

(a + b)² = a ² + 2 ab + b ²

(a + b)³ = a ³ + 3 a ² b + 3 ab ² + b ³

2) гипотеза: очевидно, коэффициенты (a + b) ⁿ равны числам n -ой строки треугольника Паскаля.

3) обоснование (доказательство) – методом математической индукции.

Метод математической индукции основан на так называемом принципе математической индукции: если какое-нибудь утверждение, сформулированное для натурального числа n, проверено для n =1 и из допущения его истинности для некоторого значения n = k следует его истинность для значения n = k + 1, то утверждение верно для любого натурального числа n.

Таким образом, метод математической индукции, применяемый к доказательству некоторой теоремы (формулы) обычно выглядит так:

1-й шаг. Проверяем истинность для п =1.

2-й шаг. Допускаем, что теорема верна для некоторого n = k и, исходя из этого допущения, доказываем истинность теоремы для n = k + 1

3-й шаг. На основании первых двух шагов доказательства и принципа математической индукции, заключаем, что теорема верна для любого натурального n.

Пример 9. Доказать, что

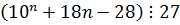
1-й шаг. Проверяем истинность для n=1:

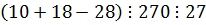- верно

2-й шаг. Допускаем, что утверждение верно для некоторого n = k

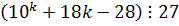
и исходя из этого допущения, доказываем истинность утверждения для

n = k + 1:

=

= =

= .

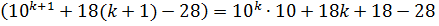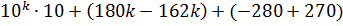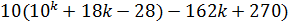Так как первое слагаемое делится на 27 по предположению индукции, а второе и третье слагаемые делятся нацело на 27, то и вся сумма делится на 27.

3-й шаг. На основании того, что данное утверждение верно для n =1 и из предположения того, что оно верно для некоторого значения n = k, доказана его истинность для значения n = k + 1, данное утверждение верно для любого натурального числа n.

В математике доминируют дедуктивные умозаключения, хотя индуктивные методы играют существенную роль. В школьном обучении математике по сравнению с математической наукой удельный вес индуктивных методов значительно возрастает. Это определяется психологическим факторами педагогического процесса, невысоким начальным уровнем познавательных возможностей детей, постепенным и длительным процессом формирования их интеллекта. Соотношение между этими методами зависит от возраста школьников. Если в начальных классах преобладают индуктивные методы, то в старших классах – дедуктивные.

Аналогия.

Аналогия примыкает к неполной индукции. Если две вещи связаны одна с другой в одном или более признаках, и если некоторое высказывание истинно относительно одной из них, то оно, возможно, истинно и относительно другой. Схема заключения по аналогии: А обладает признаками с 1, с 2, …, сn. В обладает теми же признаками с 1, с 2, …, сn. А обладает признаком d, вероятно, и В обладает признаком d.

Пример 10.

В планиметрии мы изучаем параллелограмм, в стереометрии аналогичной фигурой является параллелепипед. Противоположные стороны параллелограмма равны и параллельны, противоположные грани параллелограмма равны и параллельны. Диагонали параллелограмма, пересекаясь, делятся пополам, диагонали параллелепипеда – тоже. Наличие таких аналогичных свойств позволяет предположить, что эта аналогия распространяется и дальше. Так, сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. Пробуя проверять аналогичное утверждение для параллелепипеда, убеждаемся, что у него сумма квадратов диагоналей равна сумме квадратов всех его ребер и т.д.

Но заключение по аналогии, как и неполной индукции, нуждается в доказательстве. Учащимся надо показать ряд примеров, когда аналогия может привести к грубым ошибкам.

В планиметрии можно построить бесконечное множество правильных многоугольников с каким угодно числом сторон, в стереометрии существует всего лишь 5 правильных многогранников. В планиметрии из всех многоугольников жестким является только треугольник (многоугольник называется жестким, если, будучи сделан из твердых негнущихся стержней, подвижно скрепленных в вершинах, он не может подвергнуться деформации). В стереометрии жестким является любой выпуклый многогранник (теорема Коши) (многогранник будет жестким, если, будучи сделан из твердых негнущихся пластинок, подвижно скрепленных в ребрах, он не может подвергнуться деформации).

В планиметрии один из двух равновеликих многоугольников всегда можно разрезать на такие треугольники, из которых можно сложить другой. В стереометрии один их двух равновеликих многогранников вообще нельзя разрезать на такие тетраэдры, из которых можно сложить другой (теорема Дена – Кагана).

Разница между аналогией и индукцией состоит в том, что в индукции происходит заключение от отдельных объектов к роду, в аналогии же – от объекта к объекту, от одного класса к другому классу. Вероятность заключения по аналогии зависит от того, насколько признаки с 1, с 2, …, сn, принадлежащие А и В, преобладают над различиями между А и В: чем больше общих свойств, чем меньше различий, тем больше вероятность правильного заключения. При этом признаки, являющиеся следствием некоторого признака, не принимаются во внимание. Если В обладает признаком, несовместимым с теми признаками, на основании которых делается заключение по аналогии, то общие признаки А и В не имеют значения, и вероятность заключения по аналогии равна нулю. Если d – следствие с1, с2, …, сn, то нет надобности заключения по аналогии.

Наиболее глубоко идущей аналогией, позволяющей делать безошибочные заключения, является изоморфизм. В случае изоморфизма каждое предложение, справедливое для одного множества объектов, можно полностью и без доказательства переносить на изоморфное множество объектов. Это обстоятельство дает возможность при наличии нескольких взаимно изоморфных множеств ограничиваться детальным рассмотрением только одного из них. Так в аналитической геометрии изучение свойств фигур сводится к изучению отношений между определенными уравнениями.

Аналогия является одним из эвристических методов в процессе математического развития: может подсказать существование нового предложения, способ доказательства или решения задачи. Понятие о функции комплексного переменного создано по аналогии с функцией действительного переменного, геометрия n -мерного пространства – по аналогии с 2-мерным или 3-мерным.

Но многие математические ошибки и заблуждения учащихся объясняются неверными аналогиями:

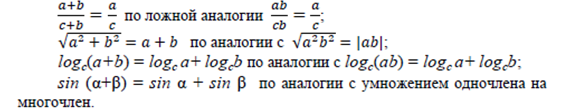
Учитель должен искоренять такие ошибки и предупреждать их появление (главное – добиваться ясного понимания основных понятий, знания содержания и объема понятия).

 

Изучения свойств арифметических действий в младших и старших классах.

1. Овладение счетом требует умения прибавлять 1 к любому числу, к полученному результату снова прибавить 1. Таким образом, сложение числа с единицей возникло с появлением счета. В дальнейшем сложение двух чисел выразилось в присчитывании к данному числу по одному всех единиц 2-го слагаемого. Таким же образом считают и дети.

Например, к 3 прибавить 2: на одной руке ребенок показывает 3 пальца, а на другой – 2. На следующем этапе обучения ребенок уже не пересчитывает единицы 1-го слагаемого, а сразу называет его и присчитывает к нему все единицы 2-го слагаемого.

Сотни лет люди древнего мира выполняли сложение подобным же образом: устно с помощью конкретных предметов, а позже с помощью специальных приборов. После изобретения позиционной системы счисления индийские математики нашли способ выполнения сложения и в письменном виде. При вычислениях они записывали числа палочкой на доске в столбик одно под другим. Сумму записывали над слагаемыми. Складывать начинали со старшего разряда. Индийский прием сложения позаимствовали математики Востока, а позднее и Европы. В конце XV века француз Н.Шюке и итальянец Л. Пачоли впервые ввели знаки сложения и вычитания: p, m (от латинского plus и minus). А немецкие математики ввели современные обозначения «+» и «–».

В Древнем Египте действие «сложение» обозначали специальным знаком ^ - рисунком шагающих ног.

Название «слагаемое» впервые встречается в работах математиков XIII века.

Термин «сумма» стал использоваться в современном значении только в XV веке. До этого он имел более широкий смысл. Суммой называли любое из четырех арифметических действий.

В Древней Индии вычитание чисел выполняли способом отсчитывания от уменьшаемого по одному, пока не получится вычитаемое: 9 - 5: 9 без 1 – 8; 9 без 2 -7; 9 без 3 – 6; 9 без 4 – 5.

Другой способ вычитания – австрийский, состоял в прибавлении к вычитаемому такого числа, которое в сумме с вычитаемым дает уменьшаемое:

9 – 5: 5 + 1= 6; 5 + 2 = 7; 5 + 3= 8; 5 + 4 = 9, значит, 9 – 5 = 4.

Понятие «разность» было введено в XV веке, а понятия «уменьшаемое», «вычитаемое» появились в Европе только в XVIII веке.

Знак деления в России в XVIII веке впервые стал использовать Магницкий.

В 1556 году английский математик Рекорд ввел знак равенства «=», которым пользуются и в настоящее время.

2. В курсе математики начальной школы находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел, в соответствии с которым сложение целых неотрицательных чисел связано с операцией объединения попарно непересекающихся множеств, вычитание – с операцией дополнения выделенного подмножества. Этот подход легко интерпретируется на уровне предметных действий, позволяя тем самым учитывать психологические особенности младших школьников.

По традиционной программе изучение сложения и вычитания в пределах 10 проводится в следующей последовательности:

1. Подготовительный этап: раскрытие смысла действий сложения и вычитания, знакомство с компонентами сложения, случаи прибавления и вычитания 1, где результаты находятся с опорой на знания образования натуральной последовательности чисел.

2. Изучение приемов присчитывания и отсчитывания по одному и группами для случаев +- 2, 3, 4.

3. Изучение переместительного закона сложения для случаев «+»5, 6, 7, 8, 9

4. Изучение взаимосвязи между компонентами для случаев «–» 5,6, 7, 8, 9.

Подготовительная работа к изучению сложения и вычитания начинается с первых уроков рассмотрения нумерации. Учащиеся должны прочно усвоить способы образования любого числа первого десятка присчитыванием и отсчитыванием единицы и, используя этот прием, свободно выполнять сложение и вычитание с единицей.

В качестве основного средства формирования представлений о смысле действий сложения и вычитания выступают простые текстовые задачи. Выполняя многократно операции над множествами, учащиеся уясняют, что операции объединения соответствует действие сложения, а операции удаления части множества – действие вычитание.

На втором этапе рассматривают случаи сложения и вычитания вида + - 2, 3, 4, результаты которых находятся присчитыванием или отсчитыванием.

Рекомендуется научить учеников находить значение выражений вида: 6 + 1 + 1; 9 – 1 – 1, иллюстрируя действия с предметами, например: «Положите 4 красных яблока, придвинь 1 желтое яблоко. Сколько яблок стало? Придвиньте еще 1 желтое. Как можно записать решение? Сколько всего яблок мы прибавили?»

Затем приступают к рассмотрению приема прибавления и вычитания числа 2. Например: «Посмотрите, сколько букетов стоит на окне? (4) Надо поставить на окно еще 2 букета (стоят в другом месте). Как узнать, сколько букетов будет на окне? Как же можно к 4 прибавить 2? (ученик по одному переносит букеты на окно). Запишем решение».

С помощью аналогичных упражнений раскрываются приемы вычислений для случаев +-3, +-4, представляя число 3 как сумму чисел 2 и 1, а число 4, как сумму чисел 2 и 2.

Завершающим моментом в работе над каждым из приемов является составление и заучивание таблиц.

На этом же этапе изучения сложения и вычитания учащиеся знакомятся с терминами: «сложение», «вычитание», «слагаемое», «сумма», а позднее – «уменьшаемое», «вычитаемое», «разность».

На третьем этапе изучают прием сложения для случаев «+»5, 6, 7, 8, 9. При сложении в пределах 10 второе слагаемое больше первого. Если при вычислениях применить перестановку слагаемых, то эти случаи сведутся к раннее изученным. Поэтому именно на этом этапе целесообразно раскрыть ученикам суть переместительного закона. Для его разъяснения могут быть использованы действия с предметными множествами, сравнение числовых равенств, в которых переставлены слагаемые, сравнение суммы длин одинаковых отрезков.

При формировании у детей представлений о смысле сложения полезно предлагать им такие ситуации для предметных действий, при выполнении которых они сами подмечают закономерности, связанные с переместительным свойством сложения. Например: «На одной тарелке 4 апельсина, на другой – 3; сколько апельсинов на обеих тарелках? Запишите решение: 4 + 3 = 7; на одной тарелке 3 апельсина, на другой – 4; сколько апельсинов на обеих тарелках?. Запишите решение: 3 + 4 = 7; Сравните эти записи: чем они похожи (оба примера на сложение, складываем одни и те же числа, получаем один и тот же результат) и чем отличаются (слагаемые поменяли местами)?

      Возможен и другой вариант моделирования переместительного свойства сложения: Т = ▲▲▲ Т + К = ▲▲▲■■

К = ■■ К + Т = ■■▲▲▲

Таким образом, на основе переместительного закона сложения оказывается рассмотренной вся таблица сложения в пределах 10, которая должна быть усвоена на память.

Следует обратить внимание учащихся на наличие в этой таблице определенных закономерностей. Например, в каждой строке оказывается отрезок натурального ряда чисел до 10. По диагоналям получаем четные числа от 2 до 10. По главной диагонали так же можно указать ряд четных и нечетных чисел. Особое внимание обращается на сложение одинаковых слагаемых.

1 2 3 4 5 6 7 8 9

1 2 3 4 5 6 7 8 9 10

2 3 4 5 6 7 8 9 10

3 4 5 6 7 8 9 10

4 5 6 7 8 9 10

5 6 7 8 9 10

6 7 8 9 10

7 8 9 10

8 9 10

9 10

 

Основным является блок, выделенный в таблице. Запоминанию подлежат следующие случаи:

2 + 2 = 4

3 + 2 = 5 3 + 3 = 6

4 + 2 = 6 4 + 3 = 7 4 + 4 = 8

5 + 2 = 7 5 + 3 = 8 5 + 4 = 9 5 + 5 = 10

6 + 2 = 8 6 + 3 = 9 6 + 4 = 10

7 + 2 = 9 7 + 3 = 10

8 + 2 =10

Остальные случаи могут быть получены, используя переместительный закон сложения.

На четвертом этапе изучается прием вычитания на основе взаимосвязи между компонентами для случаев «–» 5, 6, 7, 8, 9.

Знакомство с взаимосвязью между компонентами и результатом действия сложения можно провести следующим образом:

Положите на парту 5 красных и 4 синих кружка. Сколько всего кружков положили? Как можно записать решение? (5 + 4 = 9) Назовите компоненты суммы.

1-ое слаг. 2-ое слаг. сумма

5 + 4 = 9

Итак, на парте у вас 9 кружков. Возьмите 4 синих кружка. Сколько кружков у вас осталось? Как запишем решение? (9 – 4 = 5). Назовите компоненты, используя первую запись.

Сумма 2-ое слаг. 1-ое слаг.

9 - 4 = 5

Какой вывод можно сделать: чтобы найти 1-ое слагаемое, надо из суммы вычесть 2-ое слагаемое.

Аналогично рассматривается и другой случай. На парте у вас 9 кружков. Возьмите 5 красных кружка. Сколько кружков у вас осталось? Как запишем решение? (9 – 5 = 4). Назовите компоненты, используя первую запись.

Сумма 1-ое слаг. 2-ое слаг.

9 - 5 = 4

Какой вывод можно сделать: чтобы найти 2-ое слагаемое, надо из суммы вычесть 1-ое слагаемое.

Приступая к раскрытию нового приема вычитания, учитель предлагает ученикам объяснить, как можно найти значение выражения 10 – 8? Выслушав различные предположения, учитель ставит задачу – найти более удобный прием вычисления. Учащиеся совместно с учителем вспоминают состав числа 10, выбирают «пример-помощник» (10=8+2). Если из суммы 8 и 2 вычесть 8, получится 2.

Аналогично находят значение других выражений. На следующих уроках для выработки навыка вычислений включают разнообразные упражнения.

В процессе изучения сложения и вычитания продолжается формирование понятия о числе нуль.

Число нуль является характеристикой пустого множества, т.е. множества, не содержащего ни одного элемента. Для того чтобы учащиеся представили себе такое множество, можно использовать различные методические приёмы.

Один из приёмов связан с установлением соответствия между числовой фигурой и цифрой, обозначающей количество предметов. Этим подходом можно воспользоваться до изучения сложения и вычитания, на этапе формирования у учащихся представлений о количественном числе.

Можно предложить задания с формулировкой «Что изменилось?» и изображением количественной и пустой совокупностей предметов.

Другой методический приём знакомит учащихся с нулём как результатом вычитания. Для этой цели им предлагаются предметные ситуации, которые они сначала описывают, а затем записывают решение с помощью числовых равенств. (У девочки было 2 тетради, она отдала учителю 2 тетради. Сколько тетрадей осталось у девочки?)

Если по программе М.И. Моро в качестве основного средства формирования у учащихся представлений о смысле действий сложения и вычитания выступают простые текстовые задачи, то в основе других подходов (Н.Б Истомина, Л.Г. Петерсон) лежит выполнение учащимися предметных действий и их интерпретация в виде графических и символических моделей. В качестве основной цели выступает осознание предметного смысла числовых выражений и равенств. Деятельность учащихся сначала сводится к переводу предметных действий на язык математики, а затем к установлению соответствия между различными моделями.

Например, детям предлагается иллюстрация, на которой Миша и Маша запускают рыбок в один аквариум. Организуя деятельность учащихся с данной предметной иллюстрацией, учитель подводит учащихся к выводу о том, что рыбки Миши и Маши объединяются в одном аквариуме. Затем учитель сообщает, что действия Миши и Маши можно записать на языке математики (2 + 3; 3 + 2). Эти записи даны под иллюстрациями и являются математическими выражениями, которые в математике называют суммой. Выясняется, чем похожи эти выражения и как можно эти выражения прочитать по-разному. Помимо выражений каждой иллюстрации можно поставить в соответствие определенное число. Далее учитель показывает, как записать равенство и знакомит учащихся с этим понятием, а также с термином «значение суммы».

Затем числовые равенства интерпретируются на числовом луче.

Можно условно выделить три вида ситуаций, связанных с операцией объединения: 1) увеличение данного предметного множества на несколько предметов;

2) увеличение на несколько предметов множества, равночисленного данному;

3) составление одного предметного множества из двух данных.

В процессе выполнения предметных действий у младших школьников формируется представление о сложении как о действии, которое связано с увеличением количества предметов.

При формировании у детей представлений о вычитании можно условно ориентироваться на следующие предметные ситуации:

1) уменьшение данного предметного множества на несколько предметов;

2) уменьшение множества, равночисленного данному, на несколько предметов;

3) сравнение двух предметных множеств.

В процессе выполнения предметных действий у младших школьников формируется представление о вычитании как о действии, которое связано с уменьшением количества предметов.

В основе усвоения взаимосвязи между компонентами и результатами сложения и вычитания лежит осознание учащимися предметного смысла этих действий. При этом следует учитывать, что особую трудность для некоторых детей представляет вычленение и удаление части множества, т.е. осознание тех предметных действий, которые связаны со смыслом вычитания.

В исследовании Г.Г. Микулиной было выявлено, что значительная часть учащихся при выполнении предметных действий, связанных с вычитанием, фиксирует скорее пространственное отделение, разъединение двух множеств, чем вычленение и удаление части из целого.

Рассмотрим некоторые методические приёмы, в которых учитываются описанные выше психологические особенности младших школьников:

Работая у доски с рисунками и дидактическими пособиями, полезно сначала предложить ученику показать предметные совокупности, с которыми он действует, а затем уже назвать число предметов в них.

Выполняя задания с рисунками, к которым дана запись вида –=, рекомендуется заполнять «окошки» не только в прямом порядке, но и начиная с любого.

Можно использовать задания такого же рода, но со скрытыми количествами. При их выполнении внимание учащихся сосредотачивается на соотнесении элементов схемы и предметных совокупностей.

Осознавая взаимосвязь компонентов и результатов действий, не все дети могут описать её, пользуясь математической терминологией: слагаемые, значение суммы, уменьшаемое, вычитаемое, значение разности. В этом случае целесообразно использовать понятия целого и части и соотношение между ними (часть всегда меньше целого; если убрать одну часть, то останется другая).

Понятие целого и части позволяет как бы «материализовать» такие термины, как слагаемые, уменьшаемое, вычитаемое (например, устанавливая соответствие между рисунком и математической записью).