2020-06-10
129
Координаты вершины параболы y=ax2+bx+c можно найти с помощью уравнений.
А(х0, у0) – вершина параболы y=ax2+bx+c, где х0 находят с помощью уравнения 
, а у0=у(х0)= ax02+bx0+c.
Направление осей параболы определяется по знаку коэффициента а. Если a <0, то ветви параболы направлены вниз, а если a >0, то ветви параболы направлены вверх.
y=3x2+2+1 а=3>0, значит, ветви параболы направлены вверх.
у= –х2 а= –1<0, значит, ветви параболы направлены вниз.
Построение графика функции у=ах2+bx+c движением графика функции y=x2
Любой график функции y=ax2+bx+c можно получить из функции у=ах2.
Например, функцию у= х2 – 2х + 3 можно получить сдвигом вправо на 1 единицу и вверх на 2 единицы графика функции у=х2.
Проверим графически, действительно ли функцию у= х2 – 2х + 3 можно получить движением графика функции у=х2. Для этого построим график функции у= х2 – 2х + 3 по точкам.
Составим таблицу значений функции у= х2 – 2х + 3.
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| у= х2 – 2х + 3 | 18 | 11 | 6 | 3 | 2 | 3 | 6 |
Построим найденные точки и проведём через них плавную кривую.
Вершина параболы по отношению к графику функции у=х2 сместилась вправо на 1 единицу и вверх на 2 единицы.
Не составляя таблицы значений и построения функции по точкам, можно сразу узнать, куда сместиться вершина параболы и, проведя мысленно через эту точку координатные прямые (взяв эту точку за начало координат), а затем построив график функции у=х2, получить искомый график. Для этого необходимо преобразовать выражение y=ax2+bx+c методом выделения полного квадрата.
Как же мы до построения графика определили, что график сместился на 1 единицу и вверх на 2 единицы графика функции у=х2? Это можно сделать преобразованием уравнения.
Преобразуем у= х2–2х+3 методом выделения полного квадрата: у= х2–2х+3=
= х2–2х+1+2=(х-1)2+2. То есть наше уравнение у= х2–2х+3 мы привели к виду y=f(x+ l)+m. А чтение таких уравнений мы уже рассмотрели в предыдущем параграфе.
Построение графика функции у=ах2+bx+c, определение свойств квадратичной функции. Нахождение точек пересечения графика с осью ОХ
Научимся находить точки пересечения графика функции у= ax2+bx+c с осью ОХ.
Если график пересекает ось ОХ, значит, в точках пересечения у=0. Такие точки называют нулями функции. Для их нахождения нужно приравнять уравнение функции к нулю, затем разложить уравнение на множители вида у=а(х-х1)(х-х2) х1 и х2 – это и есть нули функции.
Найдём, например, нули функции 
. Разложим это уравнение на множители. 
. Это значит, что в точках А(-2;0) и В(3;0) график функции пересечёт ось ОХ.
Мы уже с вами выяснили, что график функции y=ax2+bx+c можно построить двумя способами: по точкам или движением графика функции у=аx2.
Разберём ещё один алгоритм построения графика функции y=ax2+bx+c, если под рукой нет шаблона для построения движением.
1. Построить вершину параболы (х0, у0), где х0 находят с помощью уравнения , а у0=у(х0)= ax02+bx0+c.
2. Провести через вершину параболы прямую, параллельную оси ординат, - ось симметрии параболы.
3. Найти нули функции (f(x)=0 - точки пересечения графика с осью ОХ), если они есть, и построить на оси абсцисс соответствующие точки параболы.
4. Построить 2 какие-нибудь точки параболы, симметричные относительно её оси. Для этого надо взять 2 точки на оси ОХ, симметричные относительно точки х0, и вычислить соответствующие значения функции. Например, можно построить точки параболы с абсциссами х=0 и х=2х0, если х0≠0 (ординаты этих точек равны с).
5. Провести через построенные точки параболу. Заметим, что для более точного построения графика полезно найти ещё несколько точек параболы.
Свойства функций мы уже неоднократно учились определять по графику. Напомним, какие это свойства:
1) область определения функции;
2) область значений функции;
3) промежутки возрастания и убывания функции;
4) точки максимума и минимума функции;
5) нули функции;
6) значения f(0).
Рассмотрим в качестве примера функцию у=х2-4х+3. Так как квадратичную функцию можно построить при любом значении х, значит, мы можем сделать вывод о том, что область определения функции D(f)= 
. Чтобы определить область значений функции, нужно представить функцию в виде y=f(x+ l)+m. у=х2-4х+3= х2-4х+4-1=(х-2)2-1. Таким образом, область значений функции E(f)= 
. Это разложение мы можем использовать для построения графика функции. Сдвинем на 2 единицы вправо и на 1 единицу вниз график функции у=х2.
Ветви параболы направлены вверх. Функция убывает на промежутке 
, а возрастает на промежутке 
. Точка (2;-1) – минимум функции. Нули функции мы можем найти, разложив уравнение нашей функции на множители. у=х2-4х+3=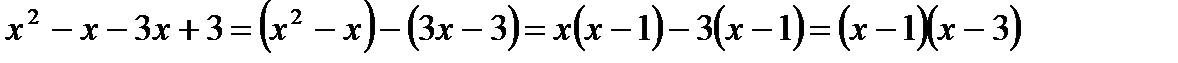 
Нули функции А(1;0) и В(3;0). Точки пересечения с осью OY: f(0). f(0)= 02-4⸳0+3=3. C(0;3) – точка пересечения с осью OY. Симметричная ей точка относительно прямой, проведённой через вершину, это точка D(4;3).
Ну и, наконец, построим график функции у=х2-4х+3.
