| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средние квадраты |
| Регрессия | Ок=^(У1-У) /-1 | т -1 | 0S 1 Oig II г«а; |
| Остаточная | й = 1(л-А) /-1 | п-т | ,2_ а п-т |
| Общая | e=i(.v,-3“) /=i | п -1 |
Средние квадраты и s (табл. 3.3) представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессий или объясняющей переменной X и воздействием неучтенных случайных факторов и ошибок; т — число оцениваемых параметров уравнения регрессии; п — число наблюдений.
Замечание. При расчете общей суммы квадратов Q полезно иметь в виду, что
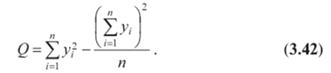
· (Формула (3.42) следует из разложения
·?? = Х(У/ -У) ='Zy? +пу с учетом (3.8).)
/=1 1=1 1=1
При отсутствии линейной зависимости между зависимой и объясняющими(ей) переменными случайные величины sr = Qr /(т ~ О и s1=Qe/(n—m) имеют /^-распределение соответственно с т— 1 и п~т степенями свободы, а их отношение — ^-распределение с теми же степенями свободы (см. § 2.3). Поэтому уравнение регрессии значимо на уровне а, если фактически наблюдаемое значение статистики
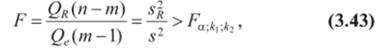
где Fa.*,.*2 — табличное значение /'-критерия Фишера—
Снедекора, определенное на уровне значимости а при к=т~ и ki=n—m степенях свободы.
1
Учитывая смысл величин si и $2, можно сказать, что значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.
В случае линейной парной регрессии т = 2, и уравнение регрессии значимо на уровне а, если

Следует отметить, что значимость уравнения парной линейной регрессии может быть проведена и другим способом, если оценить значимость коэффициента регрессии Ь, который, как отмечено в § 3.4. имеет /-распределение Стьюдента с к—п —2 степенями свободы.
Уравнение парной линейной регрессии или коэффициент регрессии Ь значимы на уровне а (иначе — гипотеза #о о равенстве параметра Pi нулю, т. е. Я0: Pi=0, отвергается), если фактически наблюдаемое значение статистики (3.37)

больше критического (по абсолютной величине), т. е.
И > Л-ot; /т-2 -
Можно показать, что для парной линейной модели оба способа проверки значимости с использованием F- и /-критериев равносильны, ибо эти критерии связаны соотношением F= /2.
В ряде прикладных задач требуется оценить значимость коэффициента корреляции г (§ 3.3). При этом исходят из того, что
гл1п — 2
при отсутствии корреляционной связи статистика / - --=-
л/l-г2
имеет /-распределение Стьюдента с п — 2 степенями свободы.
Коэффициент корреляции г значим на уровне а (иначе — гипотеза Я0 о равенстве генерального коэффициента корреляции р нулю, т. е. Но: р=0, отвергается), если
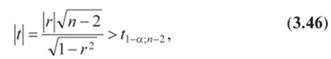
где /|_а;„_2— табличное значение /-критерия Стьюдента, определенное на уровне значимости а при числе степеней свободы п— 2.
Легко показать, что получаемые значения /-критерия для проверки гипотез р=0 по (3.45) и р=0 по (3.46) одинаковы.
? Пример 3.4.
По данным табл. 3.1 оценить на уровне а=0,05 значимость уравнения регрессии У по X
Решение. 1-й способ. Выше, в примерах 3.1, 3.2 были 10 10
найдены:? У,- = 68, = 49(3.
»=1 /=1
Вычислим необходимые суммы квадратов по формулам (3.40), (3.42):

По формуле (3.43)
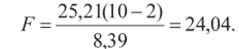
По таблице /^распределения (табл. IV приложений) /o.o5;i;8=4,20. Так как />/Ь,о5;1;8> тоУравнение регрессии значимо.
ю
2-й способ. Учитывая, что />i = l,016, ^(jc, -х) = 24,40,
/=1
s2= 1,049 (см. пример 3.3, табл. 3.2), по формуле (3.45)

По таблицам /-распределения (табл. II приложений) /0 95:8=2,31. Так как / > /Ь,95;8> то коэффициент регрессии Ь9 а значит, и уравнение парной линейной регрессии Кпо X значимы.? Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, (или, как [3]
говорят, мерой качества подгонки регрессионной модели к наблюденным значениям уд, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле

Величина R2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.
Так как 0 < Qr < Q, то 0 < R2 < 1.
Чем ближе R2 к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если R2= 1, то эмпирические точки (х,, уд лежат на линии регрессии (см. рис. 3.3) и между переменными Y и X существует линейная функциональная зависимость. Если R2= 0, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс (см. рис. 3.4).
Заметим, что коэффициент R2 имеет смысл рассматривать только при наличии свободного члена в уравнении регрессии, так как лишь в этом случае, как уже отмечалось, верно равенство (3.41), а следовательно, и (3.47).
Если известен коэффициент детерминации /?2, то критерий значимости (3.43) уравнения регрессии или самого коэффициента детерминации может быть записан в виде

В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, т. е. R2 = r2. Действительно, учитывая (3.12), (3.17),
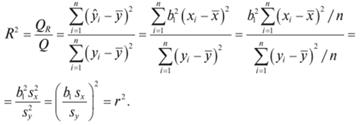
 2020-06-10
2020-06-10 109
109








