Эллипс и его каноническое уравнение

Правописание… пожалуйста, не повторяйте ошибок некоторых пользователей Яндекса, которых интересует «как построить эллибз», «отличие элипса от овала» и «эксцентриситет элебса».

Каноническое уравнение эллипса имеет вид 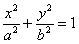, где – положительные действительные числа, причём . Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:

Как построить эллипс?

Пример 1

Построить эллипс, заданный уравнением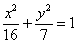

Решение: сначала приведём уравнение к каноническому виду:

Зачем приводить? Одно из преимуществ канонического уравнения 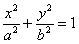заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению .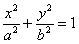

В данном случае :

Отрезок называют большой осью эллипса;
отрезок – малой осью;
число называют большой полуосью эллипса;
число – малой полуосью.
в нашем примере: .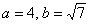

Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.

Существует два подхода к построению эллипса – геометрический и алгебраический. Из уравнения эллипса 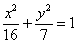на черновике быстренько выражаем:

Далее уравнение распадается на две функции:
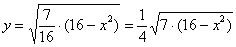– определяет верхнюю дугу эллипса;
– определяет нижнюю дугу эллипса.

Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция . Напрашивается нахождение дополнительных точек с абсциссами .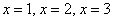
Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.

Отметим на чертеже точки (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию:

Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?

Определение эллипса. Фокусы эллипса и эксцентриситет эллипса

Эллипс – это частный случай овала. Это математический термин, имеющий развёрнутую формулировку.

Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек , называемых фокусами эллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса: .
При этом расстояния между фокусами меньше данного значения: .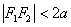

Сейчас станет всё понятнее:

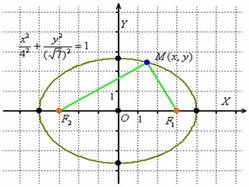
Представьте, что синяя точка «ездит» по эллипсу. Так вот, какую бы точку эллипса 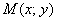мы ни взяли, сумма длин отрезков всегда будет одной и той же:

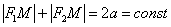
Убедимся, что в нашем примере значение суммы действительно равно восьми. Мысленно поместите точку «эм» в правую вершину эллипса, тогда: , что и требовалось проверить.