2020-06-10
2062
Если эллипс задан каноническим уравнением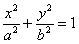 
, то его фокусы имеют координаты 
, где 
– это расстояние от каждого из фокусов до центра симметрии эллипса.
Вычисления проще пареной репы:
– это РАССТОЯНИЕ от каждого из фокусов до центра (который в общем случае не обязан располагаться именно в начале координат).
И, следовательно, расстояние между фокусами 
тоже нельзя привязывать к каноническому положению эллипса. Иными словами, эллипс можно перенести в другое место и значение 
останется неизменным, в то время как фокусы, естественно, поменяют свои координаты.
Эксцентриситет эллипса и его геометрический смысл
Эксцентриситетом эллипса называют отношение 
, которое может принимать значения в пределах 
.
Чем ближе значение эксцентриситета к нулю, тем эллипс больше похож на окружность
Окружность – это частный случай эллипса
Пример 2
Составить каноническое уравнение эллипса, если известен один из его фокусов 
и малая полуось 
(центр находится в начале координат). Найти вершины, дополнительные точки и изобразить линию на чертеже. Вычислить эксцентриситет.
|
|
|
Решение: поскольку фокусы канонически расположенного эллипса имеют координаты 
, то расстояние от каждого из фокусов до начала координат равно: 
.
По условию известно значение , из соотношения находим:
Запишем каноническое уравнение эллипса:
Вершины эллипса расположены в точках 
.
Найдём дополнительные точки:
Пример 3.
Проверить, является ли линия, заданная общим уравнением, эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия - эллипс.
Пример 4.
Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение.
Смотрим на формулу канонического уравнения эллипса и подставляем: большая полуось - это a = 5, меньшая полуось - это b = 4. Получаем каноническое уравнение эллипса:
.
