Точка, в которой сумма расстояний до сторон произвольного треугольника наименьшая

Дан треугольник ABC. Найдите внутри его точку O, для которой сумма длин отрезков OA, OB, OC минимальна. (Обратите внимание на тот случай, когда один из углов треугольника больше 120°.)

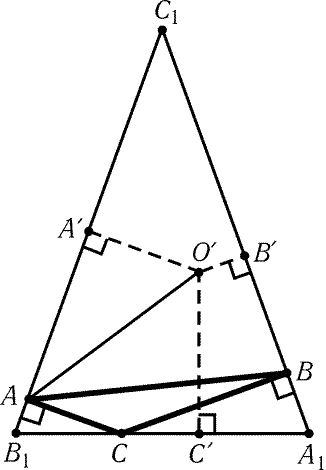
Предположим сначала, что все углы треугольника ABC меньше 120°. Тогда внутри его существует точка O,из которой все стороны видны под углом 120°. Проведем через вершины A, B и C прямые, перпендикулярные отрезкам OA, OB и OC. Эти прямые образуют правильный треугольник A ₁ B ₁ C ₁ (рис. 11.3). Пусть O - любая точка, лежащая внутри треугольника ABC и отличная от точки O. Докажем, что тогда OA + OB + OC > OA + OB + OC, т. е. O - искомая точка. Пусть A, B и C - основания перпендикуляров, опущенных из точки O на стороны B ₁ C ₁, C ₁ A ₁ и A ₁ B ₁, a - длина стороны правильного треугольника A ₁ B ₁ C ₁. Тогда OA + OB + OC = 2(S_{OB 1 C 1} + S_{O  A 1 B 1} + S_{O  A 1 C 1})/ a = 2 S_{A 1 B 1 C 1}/ a = OA + OB + OC. Так как наклонная длиннее перпендикуляра, то OA + OB + OC > OА + OB + OC = OA + OB + OC.

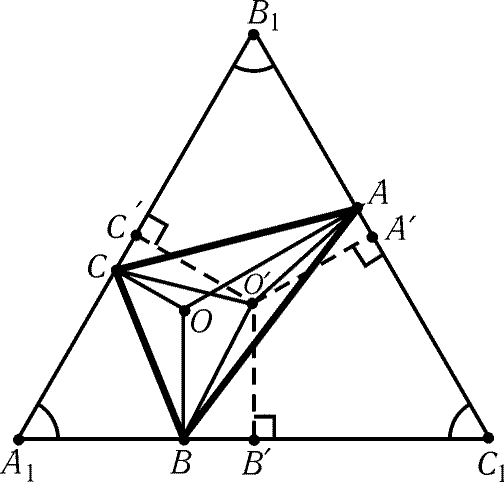
Пусть теперь один из углов треугольника ABC, например угол C, больше 120°. Проведем через точки A и B перпендикуляры B ₁ C ₁ и C ₁ A ₁ к отрезкам CA и CB, а через точку C - прямую A ₁ B ₁ перпендикулярную биссектрисе угла ACB (рис. 11.4). Так как  AC ₁ B = 180° –  ACB < 60°, то B ₁ C ₁ > A ₁ B ₁. Пусть O  - любая точка, лежащая внутри треугольника A ₁ B ₁ C ₁. Поскольку B ₁ C ₁ · O  A  + C ₁ A ₁ · O  B  + A ₁ B ₁ · O  C  = 2 S_{A 1 B 1 C 1}, то (O  A  + O  B  + O  C ) · B ₁ C ₁ = 2 S_{A 1 B 1 C 1} + (B ₁ C ₁ – A ₁ B ₁) · O  C . Так как B ₁ C ₁ > A ₁ B ₁, то сумма O  A  + O  B  + O  C  минимальна для точек, лежащих на стороне B ₁ A ₁. Ясно также, что O  A + O  B + O  C  O  A  + O  B  + O  C . Следовательно, искомой точкой является вершина C.

Точка, сумма расстояний от которой до сторон прямоугольного треугольника наименьшая

На гипотенузе AB прямоугольного треугольника ABC взята точка X; M и N - ее проекции на катеты AC и BC. При каком положении точки X длина отрезка MN будет наименьшей?

Доказательство: Так как CMXN - прямоугольник, то MN = CX. Поэтому длина отрезка MN будет наименьшей, если CX - высота.

Теорема Вивиани

Теорема Вивиани. Сумма расстояний от точки, находящейся внутри правильного треугольника, до трех сторон треугольника равна высоте треугольника независимо от выбора точки.

Эта теорема названа в честь итальянского математика Винченцо Вивиани (1622-1703), уроженца Флоренции. Галилео Галилей был настолько впечатлен талантом Вивиани, что стал работать с ним как с соавтором, когда тому было только 17 лет. Работали они вместе на вилле Арчетри, где он жил, выйдя в отставку будучи осужденным церковью, до своей смерти в 1642 году.

Винченцо Вивиани

После смерти Галилея, в 1655 году, Вивиани составил и опубликовал свою работу, а также написал биографию Галилея, которая была опубликована уже после его смерти, в 1717 году.

В Музее Истории Флоренции на картине Тито Лесси можно увидеть Галилео Галилея со своим ассистентом Винченцо Вивиани.

В 1690 году Вивиани опубликовал итальянский перевод Евклида и переводы работ Архимеда и Аполлония.

Кроме того, он изучал инженерное дело и сопротивление материалов. Совместно с Борелли он рассчитал скорость звука в воздухе, получив результат м/с. Это приближение было гораздо лучше, чем полученное ранее — м/с, в то время как в действительности скорость звука составляет м/с.

Галилей и Вивиани

Кроме того, одна кривая названа кривой Вивиани. Она определяется как пересечение цилиндра со сферой, радиус которой равен диаметру цилиндра, при условии, что цилиндр проходит через центр сферы.

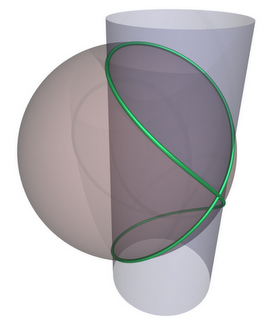
Кривая Вивиани