2020-06-10
597
1) Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Если а ^ ԃ и в ^ ԃ, то а || в.
2) Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой.
Если а || в и ԃ ^ а , то ԃ ^ в
3) Если прямая, перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости.
Если ԃ ^ b и а ^ ԃ, то а ^ b.
4) Две различные плоскости, перпендикулярные одной и той же прямой, параллельны между собой.
Если ԃ^ а и b^ а, то ԃ||b.
Признак перпендикулярности плоскостей
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Если l ^bи ԃ проходит через l, тоԃ^ b.
Свойство перпендикулярных плоскостей
Если прямая, лежащая в одной из двух взаимно перпендикулярных плоскостей, перпендикулярна линии их пересечения, то эта прямая перпендикулярна и другой плоскости.
Если ԃ^b, ԃ пересекает b по прямой n и l ^b ( l лежит в плоскости ԃ), то l ^b
Приведем обобщающую схему с уловными обозначениями для запоминания:
- признака перпендикулярности прямой и плоскости;
- признака перпендикулярности плоскостей:
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Из вершины S к плоскости квадрата ABCD проведён перпендикуляр BS и наклонные SA, SC и SD.
Назови все прямоугольные треугольники с вершиной S, обоснуй свой ответ.
Решение, рисунок: 
ABCD – квадрат, все углы которого равны по 90°.
1. Грань ASB – прямоугольный треугольник,
2. Грань BSC – прямоугольный треугольник,
т. к. BS – перпендикуляр к плоскости.
3. Грань DSC – прямоугольный треугольник, по теореме о трёх перпендикулярах:
CD⊥BC, т.к. ABCD – квадрат SB⊥BC, т.к. перпендикуляр }⇒CD⊥SC; значит, ∢SCD =90°.
4. Грань ASD – прямоугольный треугольник, по теореме о трёх перпендикулярах:
AD⊥AB, т.к.ABCD – квадрат SB⊥AB, т.к.перпендикуляр}⇒AD⊥SA;
значит, ∢SAD =90°.
Задача 2.
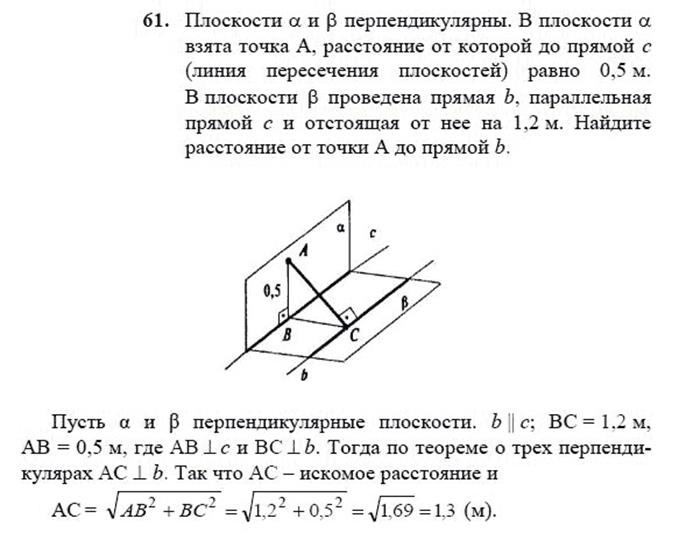Задача 3.
|
Задача 3.
ДОМАШНЕЕ ЗАДАНИЕ
1. Законспектировать в тетрадь по математике, изучить и выучить представленный материал.
2. Знать все представленные определения, признаки и свойства.
3. Внимательно рассмотреть приведенные в представленном материале решение задач и также внести решение этих задач в тетрадь по математике.
4. Выполнить домашнее задание (в тетради по математике):
Задание 1
Выбрать верное утверждение:
1) Прямая пересекает параллельные плоскости под разными углами.
2) Две прямые, перпендикулярные к одной плоскости, параллельны.
3) Длина перпендикуляра меньше длины наклонной, проведенной из той же точки.
4) Две скрещивающиеся прямые могут быть перпендикулярными к одной плоскости.
5) Угол между прямой и плоскостью может быть не больше 900.
6) Две плоскости, перпендикулярные к одной прямой, пересекаются.
7) Длина перпендикуляра больше длины наклонной, проведенной из той же точки.
