2020-06-10
535
Если проекции наклонных равны, то и сами наклонные равны.
Бо ׳ льшая наклонная имеет бо ׳ льшую проекцию
Из двух наклонных больше та, у которой проекция больше.
Вопрос 3. Перпендикулярность плоскостей
В пространстве
Пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
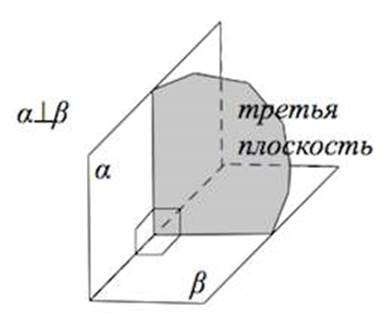
Определение перпендикулярных плоскостей можно дать и через угол между пересекающимися плоскостями.
Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90°.
Для обозначения перпендикулярности используют известный вам символ (условное обозначение) вида «
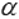». То есть, если плоскости 
и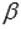 
перпендикулярны, то можно кратко записать 
.
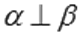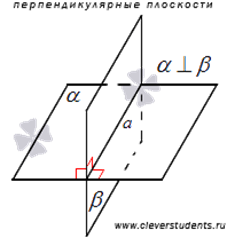
Если плоскост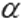и 
и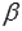 
перпендикулярны, то можно сказать, что плоскость 
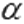перпендикулярна к плоскости 
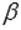и, наоборот, плоскость 
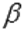перпендикулярна к плоскости 
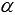. Поэтому перпендикулярные плоскости 
и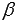 
также называют взаимно перпендикулярными.
|
|
|
Понятие угла между двумя плоскостями будет рассмотрено в следующих темах.
В качестве примера перпендикулярных плоскостей можно привести плоскости стены и пола в комнате.
Вопрос 4. Признаки перпендикулярности
Чтобы лучше понять связи между понятиями «определение», «признак», «свойство» геометрических фигур и отношений, представим эти связи в виде схемы:
 | |||
 |
 |
Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна каждой из двух пересекающихся прямых, лежащим в плоскости, то она перпендикулярна данной плоскости (см.схему).
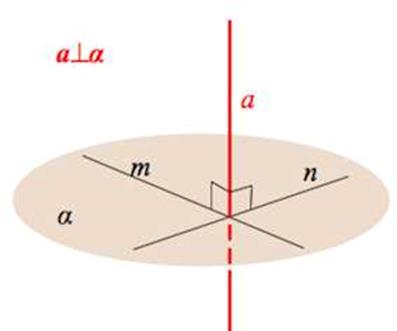
Если а ^ m и а ^ n, ( m и n ϵ плоскости ԃ), то а ^ ԃ.
