Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

 

В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими , и интенсивностью моментов с составляющими . Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.2.3) составим дифференциальные уравнения равновесия.

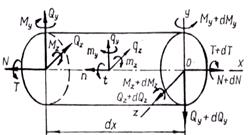
Рис. 2.3

 

Из условий следуют уравнения:

Из условий  получаем:

откуда, пренебрегая бесконечно малыми второго порядка, находим

 

 

Подставляя выражения  в соответствующие дифференциальные уравнения, получаем

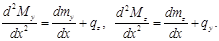
Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:

Постоянные интегрирования С_i (i =1,2,...,6) определяются из граничных условий для рассматриваемых внутренних усилий.

Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом.

Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре  определить характер эпюры . В частности, на участках, где =0 ( =0), т.е. при соблюдении зависимостей

 

 

можно установить, что при М_z = const имеем Q_y = 0(при М_y =const имеем Q_z = 0). Переменная величина  достигает экстремальных значений в точках, где Q_y = 0(Q_z = 0).

При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью.

Практикум

Примеры: 1. Построить эпюры поперечных сил и изгибающих моментов для балки (рис.2.4, а).

       а                                 б                                 в

Рис. 2.4

Решение. Определяем реакции опор А и В:

∑М_А = 20 – 10 ∙ 4 ∙ 2 – 30 ∙ 2 + R_В ∙ 6 = 0 ;  R_В = 20 кН;

∑М_В = 20 – R_А ∙ 6 + 10 ∙ 4 ∙ 4 + 30 ∙ 4 = 0;   R_А = 50 кН.

Проверка:

∑Y = 50 – 10 ∙ 4 – 30 + 20 = 0.

На 1 участке (0 ≤ х ≤ 2м):

Q_y = 50 – 10 x (прямая с граничными значениями 50 кН при х = 0 и 30 кН при х = 2 м);

М_z = –20 + 50 x – 0,5 ∙ 10 x² (парабола с граничными значениями –20 кН∙м при х = 0 и 60 кН∙м при х = 2 м).

На 2 участке (2 ≤ х ≤ 4 м):

Q_y = 50 – 10 x – 30 (прямая с граничными значениями 0 при х = 2 м и    –20кН при х = 4 м);

М_z = –20 + 50 x – 0,5 ∙ 10 x² – 30 (х – 2) (парабола с граничными значениями 60 кН∙м при х = 2 м и 40 кН∙м при х = 4 м).

На 3 участке (4 ≤ х ≤ 6м):

Q_y = 50 – 10 ∙ 4 – 30 = –20кН (прямая, параллельная оси х);

М_z = –20 + 50 x – 10 ∙ 4 (х –2) – 30 (х –2) = 120 – 20 х (прямая с граничными значениями 40 кН∙м при х = 4 м и 0 при х = 6 м).

Q_y = –20 кН и M_z = 0 при x = 6 м отражают граничные условия на опоре В.

Эпюры Q_y и M_z показаны на рис.2.4, б, в.

 

Пример 2.2. Построить эпюры N, Q и М для ломаного бруса (рис.2.5, а).

             а                      б              в                  г

Рис. 2.5

Решение. Брус имеет два участка. Первый участок – вертикальный элемент бруса (0 ≤ х ₁≤ а). Условимся нижнюю его часть считать левой частью (отмечена крестиком). Внутренние усилия в сечении с абсциссой х ₁ равны: N = 0, Q = F, M = Fx₁. При x ₁ = 0 М = 0, при х ₁ = а М = Fа.

Второй участок − горизонтальный элемент бруса (0 ≤ х ₂≤ b). В сечении с абсциссой х ₂ внутренние усилия вычисляем из условий равновесия левой части: N = F, Q = 0, М = Fа. По полученным значениям строим эпюры N, Q и М (рис.2.5, б−г).