2020-07-12
264
Расчет упругих систем на ударную нагрузку можно разбить на два этапа:
1. Определение скоростей, которые получат точки системы сразу после удара.
2. Изучение свободных колебаний системы после удара при заданном распределении начальных скоростей.
Ударное нагружение происходит тогда, когда по упругой системе ударяет масса, движущаяся с некоторой скоростью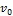 
.
Будем рассматривать в дальнейшем только неупругий или не освобождающий удар, когда ударяющее тело не отскакивает от упругой системы, по которой совершается удар, а «прилипает» к нему и совершает вместе с ним как единое целое колебательное движение. Будем считать также, что конфигурация системы при ее движении после удара считается заранее известной и неизменной.
Удар по конструкции вертикально движущимся телом
Для наглядности рассмотрим не произвольную упругую систему, а тяжелую балку (рис. 15.44, а), на которую с высоты h падает груз массой M. Выберем у балки точку C, в которой происходит удар, за точку приведения массы и заменим балку с распределенной массой d m = q d z/g (q - вес единицы длины балки, g - ускорение свободного падения) балкой с одной приведенной массой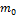 
(рис.15.44, б), т.е. заменим упругую систему с бесконечным числом степеней свободы на систему с одной степенью свободы. Обозначим через:
|
|
|
статический прогиб балки, соответствующий точке C в системе с приведённой массой, 
- жёсткость балки.
Пусть 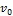- скорость падающего тела в момент удара, а v - скорость приведённой массы и «прилипшего» к нему падающего тела сразу после удара. Если груз падает с высоты h, то 
. Из условия сохранения количества движения системы имеем:
откуда
Рис. 15.44
Скорость v будет, с другой стороны, начальной скоростью объединенной массы (
) в ее колебательном движении после удара (2-й этап).
Пусть 
- статический прогиб балки в точке C от веса падающего груза Mg, т.е.
Тогда полный статический прогиб:
После удара начнётся колебательное движение упругой системы. По закону сохранения энергии сумма кинетической и потенциальной энергии системы при максимальном отклонении от статического положения равновесия перейдёт в потенциальную энергию деформации упругой системы:
где 
динамическое перемещение после удара,
т.к.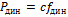 
по закону Гука; c – жёсткость упругой системы.
В результате получаем уравнение:
или, с учётом (15.133) – (15.135):
Решая полученное квадратное уравнение, находим:
где
- динамический коэффициент. (15.136)
В частности при внезапном ударе (n=0) имеем 
.
Можно иначе определить динамический коэффициент. Дифференциальное уравнение свободных колебаний системы после удара будет:
|
|
|
или
где
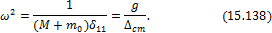
Решением уравнения (15.137) будет:
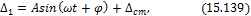
где
Закон движения (15.139) представлен на рис. 15.45.
Рис. 15.45
Начальные условия колебательного движения системы после удара
Удовлетворяя решение (15.140) этим условиям, найдем:
или
откуда находим:
Найдем теперь максимальное отклонение системы от исходного состояния в ее колебательном движении:
Соотношение (15.142) можно записать
где
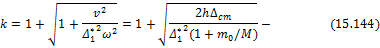
коэффициент динамичности. Он показывает во сколько раз прогиб от удара больше прогиба при статическом приложении того же груза.
Если 
то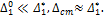 
В этом случае динамический коэффициент (105.144) принимает вид:
Выражение (15.144) совпадает с (15.136) при 
По закону Гука
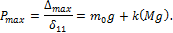
Следовательно, максимальное напряжение
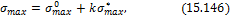
где 
- напряжение в балке до удара груза 
- статическое напряжение от груза 
При 
имеем 
