Чувствительность, селективность и их характеристики

 

     Точность результатов анализа в целом и ее отдельные составляющие, правильность и воспроизводимость, могут сильно изменяться в зависимости от состава образца. При уменьшении содержания определяемого компонента и при увеличении содержания посторонних компонентов точностные характеристики непрерывно ухудшаются, и с какого-то момента определение, а затем и обнаружение компонента оказывается вообще невозможным. Работоспособность методики в таких "экстремальных", неблагоприятных для анализа условиях характеризуют два важнейших понятия химической метрологии - чувствительность и селективность.

     Качество методики анализа, характеризующее возможность определения или обнаружения вещества в области его малых содержаний, называется чувствительностью, а в присутствии посторонних компонентов - селективностью (избирательностью). Рассмотрим основные численные характеристики чувствительности и селективности.

Чувствительность. Простейшей численной характеристикой чувствительности служит коэффициент чувствительности (S). Он определяется как производная аналитического сигнала по концентрации определяемого компонента:

 

.                                                                      (31)

 

Если градуировочная функция линейна (y = kx + b), то коэффициент чувствительности - это тангенс угла наклона градуировочной прямой k. Чем выше коэффициент чувствительности, тем меньшие содержания вещества соответствуют одной и той же величине аналитического сигнала и тем выше, при прочих равных условиях, чувствительность методики в целом.

     Однако использование величины S для описания чувствительности имеет ряд недостатков. Во-первых, коэффициент чувствительности - величина размерная, поэтому сопоставление коэффициентов чувствительности для принципиально разных (различающихся природой аналитического сигнала) методов невозможно. Во-вторых, сопоставление значений S даже одинаковой размерности имеет смысл действительно только "при прочих равных условиях", т.е. в первую очередь при одинаковой точности измерения аналитических сигналов. В то же время эта точность может меняться от методики к методике. Поэтому для характеристики чувствительности используют еще две величины, называемые пределом обнаружения и нижней границей определяемых содержаний.

     Предел обнаружения (c_min) - это наименьшее содержание вещества, которое может быть обнаружено по данной методике с заданной степенью достоверности. Таким образом, предел обнаружения (как это и следует из названия) характеризует методику с точки зрения возможностей качественного анализа.

     Предел обнаружения c_min соответствует минимальному аналитическому сигналу y_min, значимо превышающему сигнал фона y ₀ (т.е. аналитический сигнал при c =0 - с. 5). Величины аналитических сигналов для малых концентраций часто не подчиняются нормальному распределению, поэтому для оценки значимости различия между сигналами вместо строгого критерия Стьюдента (22) применяют аналогичный ему упрощенный критерий:

 

                                                                   (32)

 

Здесь s ₀= s (y ₀) - стандартное отклонение фонового сигнала, часто называемое уровнем шума. Если оно известно достаточно надежно (рассчитано из 20-25 параллельных измерений y ₀), то критерий (32) обеспечивает доверительную вероятность около 0.9 и при отклонениях распределения сигналов от нормального. Таким образом, y_min = y ₀+3 s ₀.Если градуировочная функция линейна, то, подставив это значение в уравнение градуировочной функции y = Sc+y ₀, получаем выражение для предела обнаружения:

 

.                                                                  (33)

 

Из этой формулы следует, что предел обнаружения зависит не только от коэффициента чувствительности S, но и от s ₀, т.е. точности измерения аналитических сигналов. Чем она выше, тем меньше s ₀ и c_min, тем при прочих равных условиях выше чувствительность. Обратим внимание, что величина предела обнаружения c_min имеет одну и ту же размерность – концентрация, независимо от природы аналитического сигнала.

     Для характеристики возможностей методики с точки зрения количественного анализа используют величину, называемую нижней границей определяемых содержаний (c _н). Это минимальное содержание компонента, которое можно определить с заданной степенью точности, характеризуемой предельно допустимой величиной относительного стандартного отклонения s_r (c) _max. Очевидно, что c _н> c_min. Для нахождения c _н следует определить ряд значений s_r (c) при различных концентрациях, по полученным значениям построить экспериментальную зависимость относительного стандартного отклонения s_r (c) от c (имеющую вид убывающей кривой - обычно близкой к гиперболе) и найти концентрацию, начиная с которой величины s_r (c) становятся меньше, чем заданное предельное значение s_r (c) _max (рис. 8). Иногда принимают s_r (c) _max =0.33. Однако легко показать, что в этом случае c _н» c_min, что противоречит здравому смыслу. Поэтому существуют и другие, упрощенные способы оценки c _н. В частности, часто принимают величину c _н равной k^.c_min, где коэффициент k выбирают обычно равным 2 или 3. Ввиду неоднозначности оценки нижней границы определяемых содержаний эту величину в аналитической химии используют реже, ограничиваясь, как правило, расчетом ^.c_min.

Пример 8. Рассчитать коэффициент чувствительности (мл/мкг), предел обнаружения и нижнюю границу определяемых концентраций (мкг/мл) спектрофотометрической методики определения хрома с дифенилкарбазидом, если для продукта фотометрической реакции e = 4.17^.10⁴, а измерение оптической плотности проводят в кювете с l = 1 см. Для серии измерений оптической плотности раствора контрольного опыта получены значения оптической плотности 0.006, 0.008, 0.002, 0.006, 0.010, 0.003, 0.005, 0.005, 0.012, 0.005. Нижнюю границу определяемых содержаний c _н примите равной 3 c_min.

Решение. Из уравнения градуировочной зависимости A= e lc следует, что коэффициент чувствительности равен S = e l (см. формулу (31)). Молярная масса хрома равна 52.00. Таким образом,

 

     S = 4.17^.10⁴ л^.моль^-1.см^{-1 .}1 см = 4.17^.10⁴ л/моль = 4.17^.10⁴/52.00 л/г = 802 л/г = 0.802 мл/мкг.

 

Для расчета предела обнаружения сначала рассчитаем стандартное отклонение для серии значений сигнала контрольного опыта (формула (11)):

 

     s ₀ = 0.0031

 

и затем предел обнаружения (формула (33))

 

.

 

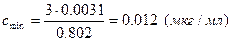Нижняя граница определяемых содержаний составляет c _н = 3 c_min. = 0.036 ~ 0.04 мкг/мл.

          Наряду с нижней границей определяемых содержаний важной характеристикой методики является и верхняя граница определяемых содержаний (c _в). Наличие верхней границы определяемых содержаний может быть обусловлено различными причинами. Одна из них – техническая невозможность измерения слишком больших значений аналитического сигнала, связанная с ограничениями измерительного прибора. Кроме того, иногда (например, при измерениях оптической плотности) в области высоких значений сигналов точность их измерения снижается. Наконец, очень часто в области высоких концентраций градуировочная зависимость искривляется (обычно отклоняясь от линейной вниз, к оси абсцисс), что также приводит к снижению точности результатов. Поэтому при описании методик анализа, как правило, указывают диапазон линейности градуировочной функции.

     Селективность. Характеристикой селективности служит коэффициент селективности k_i,j. Эта безразмерная величина равна отношению коэффициентов чувствительности двух градуировочных функций - для постороннего компонента (индекс j) и определяемого компонента (индекс i):

 

.                                                                (34)

 

Чем меньше мешающее влияние со стороны компонента j, тем меньше величина S_j, тем ниже коэффициент селективности k_i,j и тем выше селективность (таким образом, коэффициент селективности - это по существу "коэффициент мешающего влияния"). Широко распространен и практически очень удобен и другой способ описания селективности: путем указания предельного соотношения содержаний определяемого и мешающего компонента (например, 1:100), при котором еще возможно определение с заданной точностью.

Заключение

 

     Аналитическая химия – это наука о методах и средствах получения информации о составе вещества. Но любая информация представляет интерес только тогда, когда известно, насколько она достоверна. Оценка достоверности результатов – это неотъемлемая часть химического анализа, это задача не менее важная и ответственная, чем само их получение. В данном пособии рассмотрены лишь некоторые, наиболее простые, но вместе с тем и наиболее распространенные приемы, используемые для оценки качества результатов химического анализа. На практике контроль качества результатов химического анализа часто оказывается достаточно сложным. Это связано со спецификой химического анализа – многостадийной косвенной измерительной процедуры, которая включает не только операцию измерения как таковую, но и предварительные этапы пробоотбора и пробоподготовки, а также градуировку. Отдельную задачу представляет собой обеспечение качества результатов химического анализа, достижение требуемой точности. Ее решение требует множества мер не только научного, но и организационного характера. Эти мероприятия, устанавливаемые законодательно, разрабатывают и проводят в жизнь специальные отраслевые, национальные и межгосударственные службы.

     Изучением всех вопросов, связанных с измерением химических величин, методами и средствами обеспечения их единства, контроля и обеспечения качества результатов химического анализа занимается специальный раздел аналитической химии – химическая метрология. Основные правила и законы химической метрологии едины для всех методов анализа. Знание химической метрологии, умение правильно обрабатывать, оценивать и интерпретировать результаты химического анализа и, шире, любого химического эксперимента – одна из важных составляющих подготовки химика-исследователя.

Литература

 

1. Основы аналитической химии. В 2 кн. / Под ред. Ю.А.Золотова. 3-е изд. М.: Высшая школа, 2004. Кн. 1. 359 с. Кн. 2. 503 с.

2. Скуг Д., Уэст Д. Основы аналитической химии. В 2 т. М.: Мир, 1979. Т. 1. 480 с. Т. 2. 438 с.

3. Дерффель К. Статистика в аналитической химии. М.: Мир, 1994. 267 с.

4. Налимов В.В.. Применение математической статистики при анализе вещества. М.: Физматгиз, 1960. 431 с.

5. Чарыков А.К. Математическая обработка результатов химического анализа. Методы обнаружения и оценки ошибок. Л.: Химия, 1984. 168 с.

6. Дворкин В.И. Метрология и обеспечение качества количественного химического анализа. М.: Химия, 2001. 261 с.

7. Румшинский Л.З. Математическая обработка результатов эксперимента. Справочное руководство. М.: Наука, 1971. 192 с.

8. Спиридонов В.П., Лопаткин А.А. Математическая обработка физико-химических данных. М.: МГУ, 1970. 220 с.

9. Рекомендации и номенклатурные правила ИЮПАК по аналитической химии / Под ред. В.М.Иванова. М.: Бином, 2004. 160 с.

Приложение

 

Таблица 1.

Коэффициенты Стьюдента для различных чисел степеней свободы f и значений доверительной вероятности P.

 

f	P = 0.90	P = 0.95	P = 0.99
1	6.31	12.71	63.66
2	2.92	4.30	9.93
3	2.35	3.18	5.84
4	2.13	2.78	4.60
5	2.02	2.57	4.03
6	1.94	2.45	3.71
7	1.90	2.37	3.50
8	1.86	2.31	3.36
9	1.83	2.26	3.25
10	1.81	2.23	3.17
11	1.80	2.20	3.11
12	1.78	2.18	3.06
13	1.77	2.16	3.01
14	1.76	2.15	2.98
15	1.75	2.13	2.95
16	1.75	2.12	2.92
17	1.74	2.11	2.90
18	1.73	2.10	2.88
19	1.73	2.09	2.86
20	1.73	2.09	2.85
30	1.70	2.04	2.75
40	1.68	2.02	2.71
60	1.67	2.00	2.66
¥	1.65	1.96	2.58

 

Таблица 3.

Q-коэффициенты для доверительной вероятности P =0.90 и различных значений n.

 

 

n	Q	n	Q
3	0.94	7	0.51
4	0.76	8	0.47
5	0.64	9	0.44
6	0.56	10	0.41