Аксиоматический или логистический метод[215] является методом математической логики. Его содержание, коротко, заключается в том, что должен быть построен логический или формализованный язык. При его построении опираются на часть какого-нибудь обыкновенного языка, применяют ее, формируя словарь и правила языка. В этих правилах должна осуществиться теория или система логического анализа. Мы должны применять один язык, чтобы говорить о втором языке. Поэтому отличают друг от друга объект-язык и мета-язык; применение языка для того, чтобы говорить на этом языке об этом языке, не может быть методом построения формализованного языка (хотя отмечают и то, что после построения формализованного языка можно задним числом отразить в языке процесс его построения, т.е. не отрицается возможность совпадения объект-языка и мета-языка). Одним словом, посредством части какого-нибудь обыкновенного языка, исключая содержательность, строят формальную часть нового языка, этим получают неинтерпретированное исчисление или логическую систему. Более подробно это осуществляется следующим образом.
Словарь языка создается выписыванием единых символов, которые предполагается применять. Они называются начальными символами формализованного языка (таковы константы, переменные, связи и операторы, добавляют и скобки). Следует отметить, что: 1) при построении языка не используются его части и 2) начальные символы следуют друг за другом в определенной последовательности. Конечная последовательность начальных символов называется формулой. Из всех формул, согласно определенным правилам, выделяются т.н. правильно построенные формулы (только правильно построенные формулы являются высказываниями). После этого только некоторые правильно построенные формулы объявляются, аксиомами. Наконец, устанавливаются т.н. правила умозаключения, являющиеся правилами действия или превращений. Согласно этим правилам, из определенных правильно построенных формул, как из посылок, непосредственно выводятся другие правильно построенные формулы, как заключения.
Это не непосредственное умозаключение традиционной логики — выведение только из одного суждения, как из посылки (из основания) второго, как заключения (следствия), В математической логике непосредственное умозаключение понимается как выведение однократным применением одного из правил умозаключения В неинтерпретированной логической системе термины «посылка», «непосредственно вытекает» и «заключение» имеют только то содержание, которое им дается правилами умозаключения.
Конечная последовательность, состоящая из одной или нескольких правильно построенных формул, называется доказательствам, если каждая из правильно построенных формул в последовательности есть или аксиома, или непосредственно вытекает из предыдущих правильно построенных формул согласно одному правилу умозаключения.
Доказательство есть доказательство последней формулы в правильно построенной последовательности формул; а теоремами логической системы называются те правильно построенные формулы, для которых существует доказательство (в частности, каждая аксиома системы есть теорема, доказательство которой состоит из единственно правильно построенной формулы — из самой аксиомы). Вышеописанная схема, именно, начальные символы логической системы, правила, согласно части которых некоторая формула объявляется правильно построенной (правила построения), правила и аксиомы умозаключения, называется начальным базисом логической системы.
Для понимания особенностей логического метода и доказательства в математической логике необходимо учесть понятие эффективности.
Логический метод требует от мета-языка особой эффективности: 1. Данность начальных символов должна быть эффективной в том смысле, что должен, существовать метод, который всегда даст возможность эффективно определить, есть или нет какой-нибудь данный символ один начальный символ. 2. Определение правильно построенной формулы должно быть эффективным в том смысле, что должен существовать метод, всегда дающий возможность эффективно определить, правильно построена или нет какая-нибудь формула. 3. Данность аксиом должна быть эффективной в том смысле, что должен существовать метод, дающий возможность эффективно определить, есть или нет данная правильно построенная формула одна из аксиом. 4. Правила умозаключения, взятые вместе, должны быть эффективными в том строгом смысле, что должен существовать метод, который даст возможность определить, непосредственно выводится или нет правилами умозаключения данная правильно построенная формула, как заключение, из данных правильно построенных формул, как из посылок.
Из этих требований вытекает следующее: понятие доказательства эффективно в том смысле, что всегда, когда дана конечная последовательность правильно построенных формул, эффективно можно установить, является она доказательством или мет.
О первом требовании надо сказать следующее: если число начальных символов конечно, то мы легко выполним это требование, полностью переписав их. Но если их число бесконечно, то для определения начальных символов становится нужным особое указание в мета-языке. То же можно сказать и о третьем требовании, хотя иногда лучше опираться на бесконечное число аксиом.
Понятие эффективности есть интуитивно ясное математическое понятие. Говорят, что интуитивное понятие вполне достаточно для различения эффективного от неэффективного. Эффективный метод исчисления, в особенности если он расчленяется на отдельные шаги, из которых последующий зависит от результата предыдущих, называется, алгоритмом (являющимся определенной схемой). Эффективен тот метод исчисления (или алгоритм), для которого, возможно построение вычислительной машины. При неэффективности невозможно определить, имеется или нет доказательство, т.е. является ли последовательность формул доказательством.
Логическая система строится вышеописанным способом, но формализованного языка у нас не будет до тех пор, пока не указана интерпретация. А для этого нужен более широкий мета-язык. Надо применять семантические правила, которые определяют то, что обозначается формулами. Указывают на то, что для мета-языка требуется мета-метаязык.
Строгость доказательства требует отказа от использования интерпретации, его осуществления только по правилам логической системы. Это требование мотивируется следующим: 1) В вышеназванном доказательстве более точна формулировка традиционного различения формы и содержания; уточнен принцип, согласно которому правильность суждения зависит только от формы (доказательства в логической системе); форма доказательства обща для всех ее содержаний и для разных интерпретаций логистической системы. 2) Здесь выполняется требование математической строгости, согласно которому доказательство должно опираться только на аксиомы и ничто другое не должна быть использовано. Это требование расширяется тем, что доказательство опирают только на аксиомы и ход доказательства определяют только правилами умозаключения. 3)Логическая система более надежна и определенна чем интерпретации.
Отличают друг от друга неформальный аксиоматический метод и формальный аксиоматический метод. Первый применяется и рассматривается непосредственно в математике. Математические науки начинаются списком неопределенных терминов и списком постулатов, в которых эти термины содержатся и из которых средствами формальной логики выводятся теории («формальная логика» подразумевается заранее). Формальный аксиоматический метод отличается от неформального метода следующим: 1) в логистической системе начальные символы делятся на две группы: символы, которые считаются принадлежностью логики, и неопределенные термины, которые считаются принадлежностью математики. Соответственно этому и аксиомы делятся на две группы: логические аксиомы, являющиеся правильно построенными формулами, в которых подразумеваются начальные символы, и постулаты; они содержат и неопределенные термины и считаются определяющими конкретную сферу математики. Правила умозаключения, согласно обыкновенной концепции аксиоматического метода, принадлежат логике, которая лежит в основании системы. В интерпретации семантические правила также делятся на две группы: одни фиксируют общий аспект интерпретации и то, что принадлежит логике, а другие определяют остальную часть интерпретации.
Перейдем к оценке аксиоматического или логистического метода. Для математики и ее обоснования он оказался очень плодотворным. Нас здесь интересует только то, что аксиоматический метод не есть метод философской логики; он частно-научный метод, заранее подразумевающий общую логику, как определенное основание. О невозможности аксиоматизации логики будет речь ниже (§230), а здесь мы сделаем только некоторые замечания.
1. Правда, чтобы говорить об одном языке, надо использовать другой, но можно об языке говорить на том же языке; можно написать на английском языке латинскую грамматику (пример Чёрча), но ведь можно написать на английском языке и грамматику английского языка? Грузинская грамматика, написанная по-грузински, не является использованием двух языков. Рефлексивность не создает двух языков в одном и том же языке. Сам Чёрч отмечает, что возможно отождествление объекта-языка и мета-языка. Если это возможно, то рефлексивность обычного языка не делит его на два языка. Если один язык невозможен без второго и если для одного языка необходим второй, то будет невозможным понятие языка; которое может быть только одним.
Если для формализованного языка необходим мета-язык (а для того — мета-метаязык), то он (формализованный язык) имеет недостаток: а) он не может быть единственным языком, б) полная формализация будет невозможной, содержательный момент всегда будет необходим, в) общность языка разлагается, формализованный язык остается частным языком. Это означает и то, что он годен для частной науки, а не для общей логики.
2. Если правила умозаключения суть металогические правила, т.е. если они существуют за сферой логики и необходимы для математической логики, то математическая логика есть не логика, а ее применение, поскольку: а) Схема умозаключения — modus ponens — есть необходимая посылка для логистической системы. Природа modus ponens рассматривается в общей логике, а в математической только применяется, б) Если модусы первой фигуры категорического силлогизма должны быть признаны аксиомами (Лукасевич), то аксиоматически построенная система заранее подразумевает и опирается на то, что изучается, например, логикой Аристотеля; логика Аристотеля, в конце концов, есть не что иное, как выяснение природы первой фигуры силлогизма, в) Аксиомы и правила умозаключения заранее подразумевают все. Поэтому прав Чёрч, который говорит, что правила умозаключения принадлежат логике, которая лежит в основании логистической системы. Это значит, что логистическая — аксиоматическая система опирается на логику и не является ею; аксиоматический метод есть частно-научный, а не общелогический метод. Основное понятие в аксиоматической системе есть понятие функции, функционального отношения, а не понятие отношения логического основания-следствия, что и есть содержание логики.
Аксиомы, связи и метаправила для системы все подразумевают заранее. Назначение правил умозаключения состоит в выведении тавтологических положений из тавтологических же положений, в соблюдении тавтологичности[216]. Это значит, что: а) исключается необходимая для логического синтетичность, б) правила выведения, как правила действия, остаются правилами невыведения и бездействия; эти правила пригодны только для математических превращений, для превращений формул, для которых существенен способ подстановки, имеющий математически-механический характер.
3. «Посылки», «заключение», «умозаключение», «непосредственное умозаключение» и «доказательство» есть понятия общей логики, но они применяются в математической логике в другом значении, поскольку здесь не принимается во внимание основное для общей логики, а именно, отношение основания-следствия. Это последнее сведено к импликации; непосредственное умозаключение понимается как превращение, именно, как однократное применение одного правила умозаключения; а доказательство есть последовательность формул, выполненная посредством математических правил; опосредствованные связи сведены к непосредственным превращениям (так же, как Лукасевич сводит Barbara к условному предложению и т. д.). Но, главное все-таки то, что правила умозаключения объявлены посылками логики; использования схемы умозаключения в качестве посылки есть вынос умозаключения за умозаключение; представление природы умозаключения посылкой умозаключения является логической ошибкой с общелогической точки зрения. Этой ошибки нет в математической логике, так как она есть применение логики, а не сама логика. Указанная ошибка имеется тогда, когда математическую логику принимаем за общую логику и пытаемся аксиоматизировать последнюю. Начальный базис, как мы видели, представляет схему, поэтому математическая логика есть специальная наука, имеющая математический характер. Об этом свидетельствует и то, что, как было сказано, доказывается даже аксиома; это обстоятельство понятно только тогда, если общелогическое понятие доказательства заменим математическим понятием доказательства, именно, если поймем доказательство, как правильное построение формулы.
4. Сказанное станет более ясным, если вспомним одно положение Черча, указанное выше; именно, что доказательство от недоказательства мы отличаем посредством интуиции и что понятие эффективности есть интуитивно ясное математическое понятие. Это значит, что в математической логике нет логического правила, по которому можно отличить доказательство от недоказательства; в математической логике неясно, чем объясняется выбор аксиом и правил и как целиком охарактеризовать полученные из них доказанные формулы, отличающиеся вообще от формул исчисления[217]. То, что определяет общелогический метод, не может быть ни металогическим и ни интуицией, как это имеет место в логистическом методе.
5. Для уяснения характера доказательства в математической логике приведем один пример доказательства из книги Гильберта и Аккермана[218]. «Если существует сын, то существует отец», что символически выражается так:
(Ex)S(x) → (Ex)V(x),
где S(x) означает «х есть сын», a V(x) — «х есть отец». Доказательство этого предложения возможно, если мы разложим находящиеся в нем предикаты. В понятии сына подразумевается, с одной стороны, предикат «мужчина», с другой стороны отношение сына к родителям; в понятии отца подразумевается отношение к жене и к сыну. Если мы заменим «х есть мужчина» признаком М(х) и выразим предикат «х и у — родители Z» (или точнее: х и у, как муж и жена, имеют сына z) посредством символа К(х, у, z), тогда мы можем определить S(x) так:
М (х)•(Eu) (Ev) К(u, v, х)
(«х есть сын» означает «х есть мужчина, и существуют такие u и v, что u и v как муж, и как жена являются родителями х). Так же определяется V (х):
(Ey)(Ez) К(х, у, z)
(«х есть отец» означает «существуют такие у и z, что х и у как муж и жена, являются родителями z») Если мы указанные изображения подставим для S(x) и V(x), то получим следующее:
(Ex)[M(x)•(Eu)(Ev)K(u,v,x)]→(Ex)(Ey)(Ez)К(х,у,z)
Эта формула выражает отношение последовательности между двумя высказываниями; вопрос доказательства сводится к тому, чтобы от одного высказывания дойти до второго путем ряда «умозаключений», каждое из которых доказано в исчислении. Мы здесь применяем принцип, согласно которому из двух отношений предложений А→В и В→С возможно всегда заключить, что А→С.
Этот пример ясно показывает, что в математической логике доказательство есть разложение данного и установление определенных связей его частей согласно заранее данному принципу, вытекающему из обшей логики, а сами связи имеют математико-логистический характер.
6. Как известно, главная проблема математической логики есть проблема разрешимости. Проблема всегда — истинности и выполнимости, которые эквивалентны, — известна как одна проблема — проблема разрешимости. Проблема выполнимости отвечает на следующее: как должна разрешиться задача, является или нет данное выражение всегда ложным, или существуют такие высказывания, которые удовлетворяют ему, т.е. для которых оно. является истинным. Формула чистого исчисления предикатов, в которой нет никаких индивидуальных знаков, выполнима в сфере индивидуумов, если возможно заменить переменные высказывания значениями «истина» и «ложь», переменные предикаты — какими-либо специальными предикатами, которые определяются в соответствующей сфере, и свободные предметные переменные — индивидуальными предметами так, чтобы формула превратилась в истинное высказывание[219].
Получение общезначимого (тавтологического) предложения посредством таблицы осуществляется следующим образом: возьмем примеры:
|
А→А есть закон тождества, который является всегда истинным, представляет тавтологию. |
а)
| АVĀ есть закон исключенного третьего, который является всегда истинным, представляет тавтологию.
|
| А | Ā | АVĀ |
| И | Л | И |
| Л | И | И |
б)
|
|
в)
| А | В | С | А→В | В→С | (А→В)•(В→С) | А→С | [(А→В)•(В→С)]→(А→С) |
| И. | И. | И. | И. | И. | И. | И. | И. |
| И. | И. | Л. | И. | Л. | Л. | Л. | И. |
| И. | Л. | И. | Л. | И. | Л. | И. | И. |
| И. | Л. | Л. | Л. | И. | Л. | Л. | И. |
| И. | И. | И. | И. | И. | И. | Л. | И. |
| И. | И | Л. | И. | Л. | Л. | И. | И. |
| И. | Л. | И. | И. | И. | И. | И. | И. |
| И. | Л. | Л. | И. | И. | И. | И. | И. |
Это доказывает то, что гипотетический силлогизм есть всегда истинное (тавтологическое) высказывание, т.е. представляет закон.
Проблема разрешимости легко разрешается в исчислении предложений; здесь доказательство имеет чисто механический характер, как это видно из приведенной таблицы. В исчислении предложений проблема разрешимости осуществляется посредством таблиц и путем использования конъюнктивных и. дизъюнктивных нормальных форм. Но в исчислении предикатов, которое представляет главную часть математической логики, проблема разрешимости не разрешается, как это доказал Черч. В исчислении предикатов невозможно найти всеобщий разрешающий метод проблемы разрешаемости; т.е. невозможно осуществление доказательства чисто механически. Это означает то, что главная задача математической логики остается неразрешенной.
7. Как было сказано, в исчислении предикатов не разрешается проблема разрешимости; не существует полной системы тождественных (тавтологических) формул аксиом. Но в 1931 году Гёдель доказал еще больше, именно следующее: для произвольной системы основных формул и правил умозаключения можем указать на тождественные формулы, которые не могут быть выведены (вопрос касается неполности логистической системы). Согласно Гёделю, каким бы полным и всеобъемлющим не был метод доказательства, можно всегда найти предложения, которые являются истинными лишь только тогда, когда их невозможно доказать посредством данного метода. Это обстоятельство приводит нас к альтернативе: теория, более или менее богатая содержанием, является или неполной или ложной. И в самом деле, если предложения (о которых говорит Гёдель) являются истинными, тогда они не подлежат доказательству, и, следовательно, в пределах теории существуют истинные предложения, которые не могут быть доказаны посредством метода, примененного в теории.
Такая теория неполна, ее полная аксиоматизация невозможна. Если указанные предложения подлежат доказательству, тогда они ложны. Но теория, посредством которой доказываются ложные предложения, является ложной. Таким образом, доказана ограниченность логистического метода.
Здесь надо отметить и то, что расширенное исчисление предикатов, в конечном счете, приводит к трудности логической рефлексивности, разрешение которой невозможно, если мы ограничимся логикой однозначности понятия (как это отметил G. Günther). Известно то, что расширенное исчисление предикатов приводит к парадоксам, которые создаются именно рефлексивностью. Такова, например, трудность: предложение «все предложения являются или истинными или ложными» само есть одно из предложений, но оно определяется именно отношением к совокупности всех предложений.
Эта и такие трудности которые связаны с логической рефлексивностью, разрешаются только в диалектической логике, как это мы доказываем в нашем труде.
Аксиоматический метод, как это было указано и выше, опирается и исходит из природы времени и пространства. Это доказывается, в первую очередь, точкой зрения Гильберта, о которой мы коротко говорили выше, а здесь мы ее представили сравнительно более широко. Как мы знаем, с точки зрения Гильберта и Аккермана, формализм исчисления предложений и исчисления классов (исчисления одноместных предикатов, в котором подразумевается и логика Аристотеля) очень узок сравнительно с тем, что необходимо для исчисления предикатов, где основными являются отношения, каково, например, пространственное отношение между точками, именно, симметричное отношение между точками («если В находится между А и С, тогда В находится между С и А»), или такое отношение, каково отношение между сыном и отцом[220]. Мы отметили и то, что такие отношения есть отношения вещей, которые не должны входить в логику; они представляют математические отношения (отношение между величинами не есть отношение понятий, поэтому оно принадлежит математике, а не логике, то же касается и многих других отношений вещей).
То обстоятельство, что аксиоматический метод математической логики связан именно с природой времени и пространства, ясно показывает Гильберт в своем труде «Основания геометрии». Гильберт согласен с философией Канта в признании того, что логическому предшествует нелогическое, конкретные объекты, которые даются в непосредственном созерцании[221]; доказательство должно опираться на содержательно-натуральное[222]; формализованное доказательство есть конкретная и наглядная вещь[223]; «доказательство есть фигура, которая должна предстать перед нами наглядно»[224].
С указанным здесь воззрением Гильберта согласны многие современные исследователи и это они своеобразно доказывают и выражают. Так, например, Курт Вухтерл в своем труде «Чистая и математическая логика» отличает друг от друга две логики: 1) Logik als Kanon des Denkens, это есть формальная (общая) логика Канта, и 2) Logik als Organon, к которой относится и математическая логика, и которая есть применение обшей логики в конкретной сфере. Die Logik als Kanon есть предварительное основание ее любого применения, в частности и математической логики. Вухтерл отмечает что структурные теории современной математики и логистика сводятся к представлению о конструкциях чистой интуиции, которое развивается Кантом, при этом указывается на чистую чувственную интуицию (reine Anschauung) как на основание[225]. Поэтому, математическая логика, говорит Вухтерл, имеет эстетический характер (как известно, в «трансцендентальной эстетике» Канта, как в учении о времени и пространстве, т.е. как в обосновании науки математики, использован смысл греческого слова «аистезис»).
Все это, ясно, не означает того, что математическая логика опирается на субъективный идеализм Канта; нет, это означает только то, что она имеет «эстетический характер», т.е. доказательство, примененное в математической логике, опирается на природу времени и пространства и поэтому имеет математически механический характер. Как это было выяснено выше, доказательство есть последовательность формул, где умозаключения осуществляются только применением метаправил, т.е. из природы аксиом ничего не выводится без помощи внешних средств, т.е. не реализуется внутреннее необходимое следование, что для логики является главным и основным.
Следовательно, мы можем сказать, что логистический (аксиоматический) метод не есть метод общей логики, философской логики, он представляет специальный метод специальной науки. Он не есть метод философствования; он в философских трудах нигде не применяется, является лишним для них.
Гипотетический метод
«Гипотетичность», которую подразумевает гипотетический метод и о которой мы должны здесь говорить, не производится из обычно понятой «гипотезы», как из произвольного допущения положения. «Гипотетичность», подразумевающаяся гипотетическим методом, производится из греческого «гипотезиса», как из первого положения — «первого тезиса». Для этой «гипотетичности» существенна определенная необходимость, именно, необходимость первого. Необходимость «перво-положения» есть необходимость логического условия или основания, это приблизительно такая необходимость, какова необходимость категории логического, о чем мы говорили выше. Необходимость «перво-положения» заключается в том, что невозможно его неприменение, оно необходимо всегда и для всех положений в логике, в том числе и для самого себя. Здесь имеется логическая рефлексивность.
Гипотетический метод есть своеобразный метод логической рефлексии. Это метод необходимого основания, метод необходимости основания для следствия. Он представляет собой один из методов, получения необходимости основания для следствия (поэтому его нельзя отождествлять с «методом постулирования», который применяют философы современного буржуазного Запада).
Гипотетический метод сходен с методом редукции, но отличается от него, так как редукция есть необходимый переход от следствия к основанию, а в применении гипотетического метода осуществляется действие необходимого для следствия основания при полагании самого следствия. Существование следствия означает уже действие в нем основания. Здесь ни из следствия не вытекает основание, ни из основания — следствие. «Первое» как условие не существует ни после и ни только заранее. Оно есть «первое» во «втором» и «второе» — в «первом».
В истории логики и вообще в истории философии гипотетический метод применяли по-разному, хотя это был в сущности один и тот же метод. Возьмем несколько примеров, чтобы было понятно, о чем идет речь. В этом отношении образцами могут служить Платон и Кант.
1. Платон применяет гипотетический метод, заключающийся в следующем: а) для него идея есть «гипотезис», поскольку она есть определенное, своеобразное основание или «причина»[226], «первообраз» или сущность, от которой зависит все, сущностью чего она является. Эта «причина» или «первообраз» независим и действует в зависящем от него. Например, тождественные камни зависят от тождества, которое действует в них. Существование и понимание тождественных деревьев означает понимание того тождественного, которое существует независимо и само по себе, но «действует» в зависящих от него. Понятие тождественного оправдывается понятием тождества, а не наоборот. Таким образом, для Платона «гипотетичность» «действует» в существовании, в познании и в логическом. Гипотетический метод есть метод «первой философии», если выражаться словами Аристотеля. С нашей точки зрения, гипотетический метод, применяемый Платоном, есть категориальный, универсальный метод, действие которого есть «действие» категории логического.
2. Метод, применяемый в «Пармениде» Платона, есть «гипотетический метод», заключающийся в оправдании нечто его следствиями. Применение гипотетического метода есть осуществление гипотетического доказательства, которое в «Пармениде» Платона заключается в том, что принятие-непринятие нечто должно быть выведено из следствий допущения-недопущения этого нечто; следствия должны оправдать допущенное положение. В диалоге «Парменид» дана своеобразная диалектика единого и неединого, которая может быть разделена на две части: 1) допущение единого и принятие-непринятие допущенного на основании полученных отсюда следствий; 2) допущение отрицания единого и оценка допущения полученными отсюда следствиями. Более точно схема основной части «Парменида» заключается в следующем: I. Допущение единого; 1) следствия для единого, а) — при абсолютном допущении единого, б) — при относительном допущении единого, в) — при синтезе обоих этих допущений; 2) следствия для другого (неодного); а) при относительном полагании единого, б) при абсолютном полагании единого. II. Отрицание единого; 1) следствия для единого, а) при относительном отрицании единого, б) при абсолютном отрицании единого.
Как видим, диалог «Парменид» состоит из двух главных частей: 1) тезис (полагание единого), 2) антитезис (отрицание единого); но ему не хватает синтеза-результата; антитетика в этом диалоге осталась как будто неразрешенной, неразрешенным осталось то, до чего дошла антитетика, представленная в диалоге в развернутом виде, как будто цели этого диалога Платон не достиг. С нашей точки зрения, это не так. Об этом свидетельствует один фрагмент из «Государства» Платона, где говорится, что учение об едином направляет дух и возвышает его до созерцания сущего[227]. И в самом деле, с точки зрения гипотетического метода, примененного в «Пармениде» Платона, развернутая в этом диалоге антитетика должна разрешиться не в последующем, а в «перво-основании», на почве чего и применением чего она и возможна; «синтез» не в последующем, а впереди, он есть вперед допущенное первое, стоящее выше противоречия и действующее в противоречии, которое имеет смысл и возможно только на основании «первого», подлинного «сущего».
Правда, в методе, примененном в диалоге, используется и обычно понятая гипотетичность (условное допущение), но главное здесь — полагание безусловного первого.
2. Трансцендентальный метод Канта, вообще говоря, есть метод применения нечто в качестве необходимого средства. Это необходимое средство, вместе с тем, и достаточно. Оно не только априорное, но и трансцендентальное условие (время, пространство, категории, в определенном смысле — и идеи). Объяснение того способа, каким образом понятия находятся в априорном отношении к предметам, каким образом априорно принадлежат им, есть трансцендентальная дедукция[228]. Средства, которыми предметы даются в познании, есть чистые формы чувственного созерцания — время и пространство. Те средства, которыми осуществляются суждения, есть категории. Единство есть необходимое и достаточное средство для общего суждения, отрицание есть необходимое средство для отрицательного суждения и т. д. Эти средства представляют собой объективные условия. Они, в одно и то же время, являются как логическими средствами, так и средствами познания, такими логическими средствами, которые составляют необходимые условия знания.
Трансцендентальные условия, разумеется, не вытекают из того, условиями чего они являются; наоборот, они представляют предшествующие условия, но это предсуществование таково, что вне обусловленного они теряют смысл — не представляют собой того, чем они должны быть. Создание предмета этими условиями и полагание объективно значимого понятия предмета одно и то же. Существование предмета невозможно без его условий, так же как и условия представляют именно условия предмета. Общее суждение невозможно без категории единства; единство есть объективное средство — трансцендентальное условие — общего суждения, но единство представляет собой форму именно общего суждения. Единство есть, так сказать, «гипотезис» общего суждения: оно есть его сущность. Если есть условие, то есть и обусловленное. Нельзя сказать, чтобы трансцендентальное условие и обусловленное им имели независимое друг от друга существование, нет, их отношение осуществляется в одном и том же. Здесь имеется самопознание, самообоснование. Для Канта познание предмета есть то же самое, что его создание, так как мы здесь имеем дело с самопознанием, которое логически есть применение нечто в отношении самого себя. Это обстоятельство так и было понято в диалектике Фихте и Гегеля. Именно в теории диалектики было установлено, что категории, как логические формы мысли, применяются в отношении их же. В логике иначе и не может быть. Основные логические средства рефлексивны.
Гипотетический метод есть такой метод, когда полагание нечто осуществляется полаганием им же обусловленного. Если существует знание, существуют его логические условия и наоборот; если существуют логические формы, существуют и их логические условия и наоборот. Здесь имеется своеобразное действие категории логического. Это определенная логическая рефлексивность, где возможны и необходимы обращения в осново-следственных отношениях. Но гипотетический метод имеет и существенный недостаток; это — исключение отрицания, именно внутреннего отрицания, в рефлексии. Если в логической рефлексии не действует внутреннее отрицание, то логическая рефлексия будет невозможной, поскольку все будет сведено к тавтологии, которая осуществляет рефлексию только словесно. Именно вследствие этого получилось так, что трансцендентальное «я» Канта, как тавтологическое, не может быть связующим (несмотря на то, что существует и синтетическое «я»); из частного тождества ничего не вытекает. Диалектика Фихте и Гегеля идет по пути преодоления этого недостатка. В логической связи Гегель видит круг: переход от следствия к основанию и выведение следствия из основания Гегель отождествляет друг с другом; развитие представлено как возвращение к основанию.
Полная логическая рефлексивность, как мы знаем, осуществляется в бесконечном умозаключении — в самоутверждении внутренним отрицанием, где имеется самооснование и поэтому и самоследствие.
 2020-07-12
2020-07-12 223
223


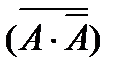 есть закон невозможности противоречия, который всегда является истинным, представляет тавтологию.
есть закон невозможности противоречия, который всегда является истинным, представляет тавтологию.






