Пусть  Тогда
Тогда 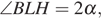 как внешний угол треугольника BLD. По теореме синусов для треугольника BHL, имеем
как внешний угол треугольника BLD. По теореме синусов для треугольника BHL, имеем

Заметим теперь, что  а
а  По теореме синусов для треугольника AHL, имеем
По теореме синусов для треугольника AHL, имеем

Значит,
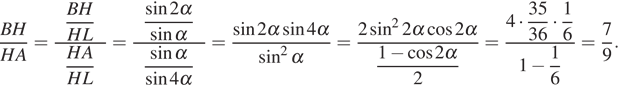
Приведем ещё одно решение.
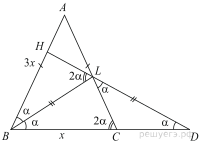
а) Обозначим  , тогда
, тогда  ,
, 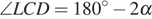 ,
, 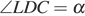 , поэтому
, поэтому 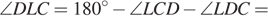
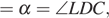 значит, треугольник LCD — равнобедренный.
значит, треугольник LCD — равнобедренный.
б) Пусть H — точка пересечения DL с AB. Тогда

поэтому  по двум углам. Отсюда
по двум углам. Отсюда 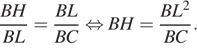
Поскольку 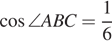 , то
, то 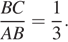 Пусть BC = x, AB = 3 x. По теореме о биссектрисе
Пусть BC = x, AB = 3 x. По теореме о биссектрисе  откуда находим
откуда находим 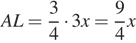 ,
,  Тогда
Тогда

значит,  , откуда
, откуда 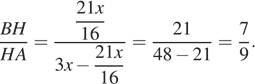
17. Первичная информация разделяется по серверам №1 и №2 и обрабатывается на них. С сервера №1 при объёме t 2 Гбайт входящей в него информации выходит 20 t Гбайт, а с сервера №2 при объёме t 2 Гбайт входящей в него информации выходит 21 t Гбайт обработанной информации, 25 < t < 55. Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 Гбайт?
Решение.
Пусть на сервере №1 обрабатывается 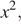 а на сервере №2 обрабатывается
а на сервере №2 обрабатывается  Гбайт из всей первичной информации. Тогда
Гбайт из всей первичной информации. Тогда 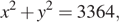 а обработано будет
а обработано будет  Гбайт информации. Требуется найти максимум суммы
Гбайт информации. Требуется найти максимум суммы  при условии
при условии

Так как 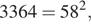 то
то 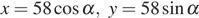 для некоторого угла
для некоторого угла  Так как
Так как 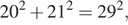 то
то
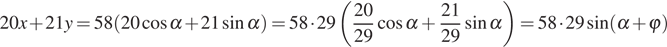
для некоторого вспомогательного угла 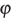 с
с 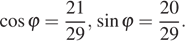 Следовательно, наибольшее значение суммы
Следовательно, наибольшее значение суммы 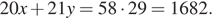 Оно достигается при
Оно достигается при 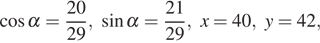 то есть для значений, удовлетворяющих условиям
то есть для значений, удовлетворяющих условиям 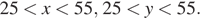
Приведём другое решение.
Пусть на сервере №1 обрабатывается  а на сервере №2 обрабатывается
а на сервере №2 обрабатывается  Гбайт из всей первичной информации. Тогда
Гбайт из всей первичной информации. Тогда 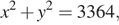 а обработано будет
а обработано будет  Гбайт информации. Выразим
Гбайт информации. Выразим 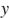 через
через  Требуется найти наибольшее значение функции
Требуется найти наибольшее значение функции 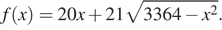
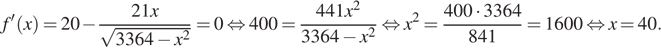
Нетрудно заметить, что  — точка максимума функции, при этом
— точка максимума функции, при этом  Условия
Условия 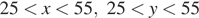 выполнены. Значит,
выполнены. Значит, 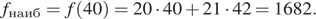
Приведём третий вариант решения.
Пусть на сервере №1 обрабатывается  а на сервере №2 обрабатывается
а на сервере №2 обрабатывается  Гбайт из всей первичной информации. Тогда
Гбайт из всей первичной информации. Тогда 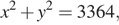 а обработано будет
а обработано будет 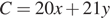 Гбайт информации.
Гбайт информации.
Так как 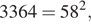 то уравнение
то уравнение 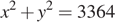 задает окружность радиуса
задает окружность радиуса 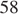 с центром в начале координат. Заметим, что уравнение
с центром в начале координат. Заметим, что уравнение 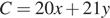 задает семейство параллельных прямых. Мы ищем наибольшее значение
задает семейство параллельных прямых. Мы ищем наибольшее значение 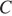 такое, что прямая
такое, что прямая  имеет общие точки с окружностью. Из всех прямых семейства пересекающих окружность, наибольшее значение
имеет общие точки с окружностью. Из всех прямых семейства пересекающих окружность, наибольшее значение  будет достигаться в случае касания.
будет достигаться в случае касания.
Проведем из начала координат в первый координатный квадрант вектор 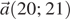 перпендикулярный прямым
перпендикулярный прямым 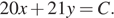 Луч, коллинеарный вектору
Луч, коллинеарный вектору  пересечёт окружность
пересечёт окружность 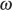 в точке
в точке 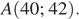 Это и будет точка касания в которой достигается наибольшее значение
Это и будет точка касания в которой достигается наибольшее значение 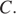 Условия
Условия 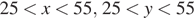 для точки
для точки 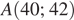 выполнены. Значит,
выполнены. Значит, 
Ответ: 1682.
18. Найдите все такие значения параметра a, при каждом из которых наименьшее значение функции 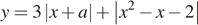 меньше 2.
меньше 2.
Решение.
Данная функция определена и непрерывна на множестве действительных чисел и точки  разбивают действительную ось на промежутки, в каждом из которых графиком данной функции является часть некоторой параболы. Заметим, что при
разбивают действительную ось на промежутки, в каждом из которых графиком данной функции является часть некоторой параболы. Заметим, что при  значения данной функции неограниченно возрастают. Следовательно, свое наименьшее значение данная функция принимает в одной из точек (или в нескольких этих точках)
значения данной функции неограниченно возрастают. Следовательно, свое наименьшее значение данная функция принимает в одной из точек (или в нескольких этих точках) 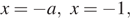
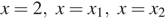 где
где 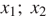 — абсциссы вершин тех парабол, ветви которых направлены вверх.
— абсциссы вершин тех парабол, ветви которых направлены вверх.
Эти параболы 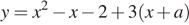 и
и 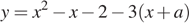 или
или  и
и 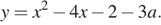 Абсциссы их вершин соответственно
Абсциссы их вершин соответственно 
Таким образом, наименьшее значение функции  меньше 2 тогда и только тогда, когда выполняется хотя бы одно из неравенств:
меньше 2 тогда и только тогда, когда выполняется хотя бы одно из неравенств: 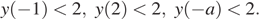
Так как  получаем совокупность неравенств:
получаем совокупность неравенств:
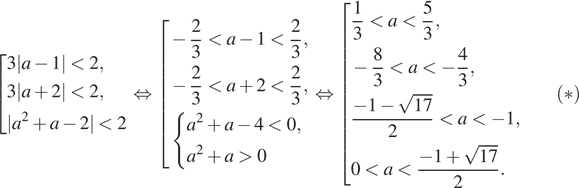
Учитывая, что 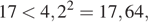 получаем
получаем 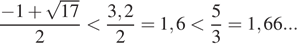
Аналогично 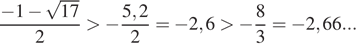
Таким образом, окончательно получаем 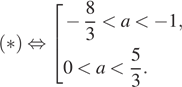
Ответ: 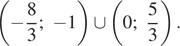
19. Участники одной школы писали тест. Результатом каждого ученика является целое неотрицательное число баллов. Ученик считается сдавшим тест, если он набрал не менее 73 баллов. Из-за того, что задания оказались слишком трудными, было принято решение всем участникам теста добавить по 5 баллов, благодаря чему количество сдавших тест увеличилось.
а) Могло ли оказаться так, что после этого средний балл участников, не сдавших тест, понизился?
б) Могло ли оказаться так, что после этого средний балл участников, сдавших тест, понизился, и средний балл участников, не сдавших тест, тоже понизился?
в) Известно, что первоначально средний балл участников теста составил 80, средний балл участников, сдавших тест, составил 90, а средний балл участников, не сдавших тест, составил 65. После добавления баллов средний балл участников, сдавших тест, стал равен 93, а не сдавших — 69. При каком наименьшем числе участников теста возможна такая ситуация?
Решение.
а) Пусть было 3 участника, которые набрали 90, 72 и 2 балла. Средний балл участников, не сдавших тест 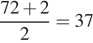 балла. После добавления баллов у участников оказалось 95, 77 и 7 баллов. Средний балл участников, не сдавших тест, составил 7 баллов.
балла. После добавления баллов у участников оказалось 95, 77 и 7 баллов. Средний балл участников, не сдавших тест, составил 7 баллов.
б) В примере предыдущего пункта средний балл участников теста, сдавших тест, первоначально составлял 90 баллов, а после добавления баллов составил  баллов.
баллов.
в) Пусть всего было N участников теста, сдали тест a участников, после добавления баллов сдали тест b участников. Заметим, что средний балл после добавления составил 85. Имеем два уравнения: 80 N = 65(N − a) + 90 a и 85 N = 69(N − b) + 93 b, откуда 15 N = 25 a, то есть 3 N = 5 a, и 16 N = 24 b, то есть 2 N = 3 b. Поэтому целое число N делится на 5 и на 3, то есть делится на 15. Таким образом, N ≥ 15.
Покажем, что N могло равняться 15. Пусть изначально 5 участников набрали по 64 балла, 1 участник — 70 баллов и 9 участников по 90 баллов. Тогда средний балл был равен 80, средний балл участников, сдавших тест, был равен 90, а средний балл участников, не сдавших тест, был равен 65. После добавления средний балл участников, сдавших тест, стал равен 93, средний балл участников, не сдавших тест, стал равен 69. Таким образом, все условия выполнены.
Ответ: а) да; б) да; в) 15.
 2020-06-29
2020-06-29 83
83







