2020-06-29
79
‑Для средней величины:
Средняя ошибка средней при собственно случайном и механическом методах отбора, (
):
а) повторный отбор:
| (3.4.1) |
б) бесповторный отбор:
| (3.4.2) |
где n — численность выборочной совокупности;
N — численность генеральной совокупности;
s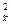 
— дисперсия средней, рассчитанная по данным выборочного наблюдения;
— доля выборки.
Дисперсия средней (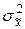
) находится с использованием формул (3.3.4-3.3.8), в зависимости от требований, указанных в задании.
Предельная ошибка выборочной средней, (D ):
D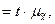 
| (3.4.3) |
где t — коэффициент кратности (доверия), зависит от вероятности (Р), с которой можно гарантировать, что предельная ошибка (D ) не превысит t – кратную среднюю ошибку ( ):
при Р = 0.683 - t = 1;
Р = 0.954 - t = 2;
Р = 0.997 - t = 3.
Доверительный интервал для средней в генеральной совокупности:
| (3.4.4) |
где 
— средняя в выборочной совокупности;
— средняя в генеральной совокупности.
‑ Для доли единиц совокупности:
Средняя ошибка доли при собственно случайном и механическом методах отбора, ( 
):
|
|
|
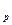а) повторный отбор:
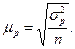
| (3.4.5) |
б) бесповторный отбор:
| (3.4.6) |
где n — численность выборочной совокупности;
N — численность генеральной совокупности;
s 
— дисперсия выборочной доли, рассчитанная по данным выборочного наблюдения;
— доля выборки.
Дисперсия выборочной доли 
находится с помощью формулы (3.3.9), которая используется для расчета дисперсии альтернативного признака.
Предельная ошибка выборочной доли (D ):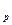
| (3.4.7) |
Доверительный интервал для доли единиц в генеральной совокупности:
 .
| (3.4.8) |
Ряды динамики
Основные показатели анализа ряда динамики:
Абсолютный прирост уровня ряда динамики:
| а) цепной |  ;
| (3.5.1) |
| б) базисный |  ,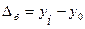
| (3.5.2) |
где 
— уровень изучаемого периода;
— уровень предшествующего периода;
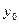— значение уровня ряда, принятое за базисное.
Темп роста уровня ряда динамики:
| а) цепной |  ;
| (3.5.3) |
| б) базисный |  .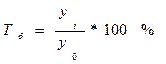
| (3.5.4) |
Темп прироста уровня ряда динамики, в %:
| а) цепной |  ;
| (3.5.5) |
| б) базисный |  .
| (3.5.6) |
Или:
Темп прироста уровня ряда динамики, в коэффициентах:
| а) цепной |  ;
| (3.5.7) |
| б) базисный |  .
| (3.5.8) |
Абсолютное значение 1 % прироста:
 .
| (3.5.9) |
Взаимосвязь показателей анализа ряда динамики:
 ;
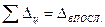| (3.5.10) |
 ;
| (3.5.11) |
 ,
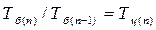| (3.5.12) |
где 
— сумма цепных абсолютных приростов;
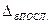— значение базисного абсолютного прироста, стоящего последним в ряду динамики;
— произведение всех цепных темпов роста;
— значение базисного темпа роста, стоящего последним в ряду динамики.
‑Основные формулы расчета среднего уровня ряда динамики, (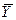
):
|
|
|
Для интервальных рядов динамики:
| а) с равными интервалами |  ;
| (3.5.13) |
| б) с неравными интервала- ми |  ,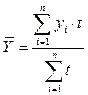
| (3.5.14) |
где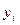 
— абсолютные уровни ряда;
n — число уровней ряда;
t — веса, длительность интервалов времени между смежными датами.
Для моментных рядов динамики:
| а) с равностоящими уровнями | |
 ,
| (3.5.15) |
| б) с неравностоящими уровнями: ‑когда нет полных данных обо всех происходящих переменах | |
 ;
| (3.5.16) |
| ‑когда есть данные обо всех происходящих переменах | |
 ,
| (3.5.17) |
где 
— рассчитанный уровень ряда, который остаются неизменным в течении времени t.
‑Средние показатели ряда динамики. Рассчитываются по интервальным рядам динамики с равными интервалами:
Средний абсолютный прирост, (
):
 .
| (3.5.18) |
Средний темп роста, в коэффициентах:
| (3.5.19) |
| (3.5.20) |
| (3.5.21) |
где П — означает произведение всех цепных темпов роста;
Т 
— значение базисного темпа роста, стоящего n ‑ным в ряду динамики;
Средний темп прироста, в коэффициентах:
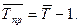
| (3.5.22) |
Индексы
Индивидуальные индексы:
| а) индивидуальный индекс объема | |
 ;
| (3.6.1) |
| б) индивидуальный индекс цены | |
 ;
| (3.6.2) |
| в) индивидуальный индекс себестоимости | |
 ,
| (3.6.3) |
где 
— объем производства за отчетный и базисный периоды соответственно;
— цена единицы продукции (товара) за отчетный и базисный периоды соответственно;
— себестоимость единицы продукции за отчетный и базисный периоды соответственно.
Общие индексы (взвешенные агрегатные индексы):
| а) общий индекс товарооборота (стоимости) | |
 ;
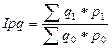| (3.6.4) |
| б) общий индекс цены (индекс Пааше) | |
 ;
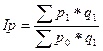| (3.6.5) |
| в) общий индекс физического объема (индекс Ласпейреса) | |
 ;
| (3.6.6) |
| г) общий индекс затрат на производство | |
 ;
| (3.6.7) |
| д) общий индекс себестоимости | |
 ;
| (3.6.8) |
| е) общий индекс физического объема (взвешенный по себестоимости) | |
 .
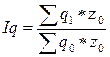| (3.6.9) |
Общие индексы, рассчитанные как средневзвешенные величины из индивидуальных индексов:
| а) преобразование агрегатного индекса количественного показателя в среднеарифметический индекс | ||
  ;
| 
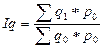| (3.6.10) |
| б) преобразование агрегатного индекса качественного показателя в среднегармонический индекс | ||
 ;
 ;
| 
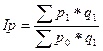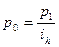| (3.6.11) |
Индекс переменного состава:
 ;
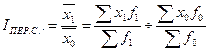| (3.6.12) |
Индекс постоянного (фиксированного) состава:
 ;
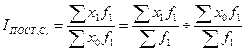| (3.6.13) |
Индекс структурных сдвигов:
 ,
| (3.6.14) |
где 
— усредненное значение изучаемого признака, рассчитанное по формуле средней арифметической взвешенной, за отчетный и базисный периоды соответственно;
— значение усредняемого показателя за отчетный и базисный периоды соответственно;
— веса (частоты или частности) каждого значения изучаемого признака за отчетный и базисный периоды соответственно.
Взаимосвязь индексов:
 ;
| (3.6.15) |
 ;
| (3.6.16) |
 .
| (3.6.17) |
При решении задач варианты и частоты заменяются на цену, себестоимость и объемс использованием тождеств:
 ,
| (3.6.18) |
 .
| (3.6.19) |
