Основные формулы для решения задач

Статистические показатели

Относительный показатель планового задания, ():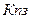

(3.1.1)

где — запланированный уровень на отчетный период;

— фактически достигнутый уровень за базисный период.

 

Относительный показатель выполнения плана, ():

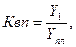
(3.1.2)

где 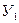— фактически достигнутый уровень отчетного периода.

 

Относительный показатель динамики, ():

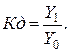
(3.1.3)

 

Взаимосвязь показателей:

(3.1.4)

Средние величины

 

Форма средней =.

(3.2.1)

 

Средняя арифметическая, ():

а) простая: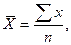

(3.2.2)

 

б) взвешенная: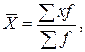

(3.2.3)

где f — веса (частоты или частности) каждого варианта.

 

Средняя гармоническая, ():

а) простая: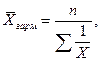

(3.2.4)

 

б) взвешенная: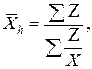

(3.2.5)

где Z = X*f.

 

Средняя геометрическая, ():

(3.2.6)

где П — знак произведения.

 

Расчет среднего процента выполнения плана, ():

а) по формуле средней арифметической взвешенной:
;	(3.2.7)
б) по формуле средней гармонической взвешенной:
,	(3.2.8)

 

Расчет среднего процента продукции высшего качества (сорта),():

а) по формуле средней арифметической взвешенной:
;	(3.2.9)
б) по формуле средней гармонической взвешенной:
,	(3.2.10)

где — объем продукции высшего качества (сорта);

  — удельный вес продукции высшего качества в общем объеме фактически выпущенной продукции.

 

Расчет среднего процента бракованной продукции ():

а) по формуле средней арифметической взвешенной:
;	(3.2.11)
б) по формуле средней гармонической взвешенной:
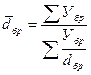,	(3.2.12)

где — объем бракованной продукции;

  — удельный вес бракованной продукции в общем объеме фактически произведенной продукции.

 

Расчет средней арифметической «способом моментов» для интервальных рядов распределения:

(3.2.13)

где i — величина интервала;

  m ₁ — момент первого порядка.

 

При этом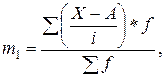

(3.2.14)

где 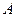— условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой.

 

Структурные средние для интервальных рядов распределения:

а) мода для интервальных рядов распределения, ():

(3.2.15)

где Х_m — начальное значение интервала, содержащего моду;

i_m — величина модального интервала;

f_m — частота модального интервала;

f_m-1 — частота интервала, предшествующего модальному;

f_m+1 — частота интервала, следующего за модальным.

 

б) медиана для интервальных рядов распределения, ():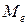

(3.2.16)

где Х_mе — начальное значение интервала, содержащего медиану;

i_mе — величина медианного интервала;

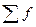— сумма частот ряда;

S_me-1 — кумулятивная частота интервала, предшествующих медианному;

f_mе — частота медианного интервала.

Показатели вариации

Размах вариации, ():

(3.3.1)

 

Среднее линейное отклонение, ():

а) для несгруппированных данных:

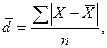
(3.3.2)

 

б) для сгруппированных данных:

(3.3.3)

Дисперсия, (s²):

а) простая дисперсия для несгруппированных данных:

(3.3.4)

 

б) взвешенная дисперсия для вариационного ряда, общая дисперсия:

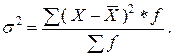
(3.3.5)

 

Упрощенные методы расчета дисперсии:

а) метод электронно-вычислительного способа расчета:

(3.3.6)

 

б) По «способу моментов»:

(3.3.7)

где m₂ — момент второго порядка, определяемый по формуле:

 

(3.3.8)

где m₁ — момент первого порядка, определяемый по формуле (3.2.14).

 

Дисперсия альтернативного признака, ():

(3.3.9)

где W — доля единиц, обладающих альтернативным признаком.

 

При этом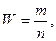

(3.3.10)

где m — количество единиц, обладающих альтернативным признаком;

n — численность единиц совокупности.

 

Среднее квадратическое отклонение, (s):

(3.3.11)

 

Правило сложения дисперсий:

(3.3.12)

где s² — общая дисперсия;

— средняя из внутригрупповых дисперсий;

d² — дисперсия групповых средних (межгрупповая) дисперсия.

 

Средняя из внутригрупповых дисперсий:

(3.3.13)

где — групповые дисперсии;

  — численность единиц в i‑ой группе.

 

Внутригрупповые дисперсии:

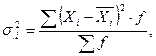
(3.3.14)

где — групповые средние;

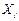— варианты внутри групп;

— частота варианта .

 

Межгрупповая дисперсия:

(3.3.15)

где — общая средняя;

— численность единиц в i‑ой группе.

 

Коэффициент вариации, ():

(3.3.16)

 

Коэффициент детерминации, ():

(3.3.17)

 

Эмпирическое корреляционное отношение, ():

(3.3.18)