2020-06-29
253
Рассмотрим среднее время жизни уровня относительно спонтанного перехода. Пусть имеются два уровни i и j. Пусть в термостате за время dt распалось 
атомов. Убыль атомов 
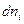согласно теории Эйнштейна пропорциональна 
, 
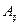и dt:
где 
– количество всех атомов в возбужденном состоянии (в момент времени t).
Интегрируя, находим
,
где 
– постоянная интегрирования – число атомов в возбужденном состоянии при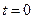 
.
Определим среднее время 
жизни атома в возбужденном состоянии:
.
Следовательно, среднее время жизни 
, - это есть время, за которое число частиц на i -м уровне уменьшится в е раз, а 
. В оптическом диапазоне при спонтанном переходе 
.
Аналогично имеем, что среднее время жизни атома относительно индуцированного перехода равно 
.
Если переход из определенного атомного состояния может происходить в результате различных процессов, характеризующихся временами жизни 
, и эти процессы статистически независимы, то время жизни данного возбужденного состояния 
связано со временами жизни для этих процессов соотношением
,
В атомной физике долгоживущие возбужденные состояния обычно называют метастабильными.
Правило отбора для дипольного излучения
Может оказаться, что некоторые из матричных элементов переходов 
(
) равны нулю. Тогда переход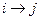 
под действием света не реализуется и излучение соответствующей частоты 
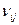в дипольном приближении не поглощается и не излучается, несмотря на то, что уровни 
и 
существуют, т.к. вероятность такого перехода равна нулю. В таком случае говорят о правиле отбора (определяемом условием 
), т.е. о правиле, которое как бы отбирает из числа всех мыслимых переходов 
только некоторые, которые в действительности реализуются. Нельзя сказать, что эти переходы не могут произойти, просто вероятность такого перехода практически равна нулю. Эти переходы могут, например, также осуществляться в результате столкновения с электронами.
