Для анализа квантовых систем можно применять вероятностный метод, основанный на описании происходящих физических явлении с использованием введенных Эйнштейном коэффициентов  ,
, 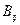 и
и 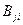 , имеющих вероятностный характер. Это вполне логично, т.к. квантовой теории внутренне присуща статистическая природа.
, имеющих вероятностный характер. Это вполне логично, т.к. квантовой теории внутренне присуща статистическая природа.
Опираясь на статистический характер происходящих в квантовых системах процессов, рассмотрим кинетику процесса в k -уровневой квантовой системе, состоящей из n квантовых частиц. Составим уравнения, описывающие распределение квантовых частиц по энергетическим уровням, считая, что коэффициенты Эйнштейна  ,
, 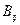 и
и 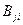 (
( ,
,  ) заданы.
) заданы.
Однако надо учесть, что помимо переходов, связанных с излучением или поглощением излучения, могут происходить и так называемые неоптические переходы, за счет которых осуществляется переход квантовой системы с одного энергетического уровня на другой без излучения или поглощения кванта энергии (такой переход может быть обусловлен различными причинами, например, соударениями и др.).
Если обозначить вероятность неоптического перехода в единицу времени квантовой системы с i -го уровня на j -й через  то полная вероятность перехода квантовой системы записывается в виде
то полная вероятность перехода квантовой системы записывается в виде
 , (10.9)
, (10.9)
где  – плотность тепловой радиации, зависящая от температуры T, при которой находятся квантовая система (температуры среды).
– плотность тепловой радиации, зависящая от температуры T, при которой находятся квантовая система (температуры среды).
В случае если переход осуществляется с нижнего уровня на верхний
 . (10.10)
. (10.10)
Следует помнить, что в формулах (10.9) и (10.10) вероятность перехода  представляет собой сокращенную запись интеграла
представляет собой сокращенную запись интеграла
 ,
,
где  – спектральная плотность излучения,
– спектральная плотность излучения,
 – спектральный коэффициент Эйнштейна,
– спектральный коэффициент Эйнштейна,
 – полуширина спектральной линии.
– полуширина спектральной линии.
Для вещества с узкими спектральными линиями, облучаемого светом широкого спектрального состава,
 ,
,
где  – частота максимума спектральной линии. Вероятности переходов
– частота максимума спектральной линии. Вероятности переходов  ,
,  ,
,  и
и  связаны соотношениями:
связаны соотношениями:
 .
.
Учитывая сказанное, запишем уравнения, определяющие скорость изменения числа квантовых частиц (изменение числа частиц в единицу времени) на энергетических уровнях k -уровневой квантовой системы. Такие уравнения называются кинетическими, т.к. они описываю кинетику происходящего процесса.
Система кинетических уравнений имеет вид
 , (10.11)
, (10.11)
где 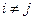 ,
,  .
.
Первое слагаемое в правой части определяет число квантовых частиц, которое уходит в единицу времени с i -го уровня на все остальные  уровни, второе же слагаемое характеризует число частиц, приходящих в единицу времени на j -й уровень со всех остальных уровней квантовой системы.
уровни, второе же слагаемое характеризует число частиц, приходящих в единицу времени на j -й уровень со всех остальных уровней квантовой системы.
Из k уравнений (10.11) независимыми являются только  уравнение. Полная система независимых уравнений, описывающих данную квантовую систему, получится, если учесть, что полное число частиц в квантовой системе неизменно и равно n, т.е.
уравнение. Полная система независимых уравнений, описывающих данную квантовую систему, получится, если учесть, что полное число частиц в квантовой системе неизменно и равно n, т.е.  . Таким образом полная система уравнений, определяющая число частиц на уровнях имеет вид:
. Таким образом полная система уравнений, определяющая число частиц на уровнях имеет вид:
 (10.12)
(10.12)
Решая систему дифференциальных уравнений (10.12), можно проанализировать, как меняется число частиц на энергетических уровнях данной квантовой системы, т.е. исследовать происходящий переходной процесс. Часто большой интерес представляет распределение числа частиц на энергетических уровнях в установившемся процессе, т.е. когда среднестатистическое число частиц на уровне в единицу времени не меняется, т.е. сколько частиц уходит с уровня, столько на него и приходит (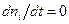 ).
).
Тогда система дифференциальных уравнений переходит в систему линейных алгебраических уравнений, решение которых записывается в следующем виде:
 ,
,
где
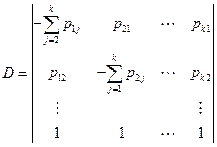 ,
,
главный определитель системы,  - определитель, полученный из главного при замене в нем i – го столбца на столбец левых частей системы:
- определитель, полученный из главного при замене в нем i – го столбца на столбец левых частей системы:
 .
.
Раскрывая этот определитель по элементам i – го столбца получаем:  , где
, где
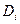 - определитель k-1 - го порядка:
- определитель k-1 - го порядка:
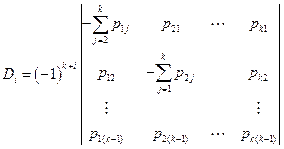
Таким образом, окончательно получаем
 (10.13)
(10.13)
В частном случае при 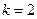 находим:
находим:
 ,
,
 .
.
Для  :
:
 ,
,
 ,
,
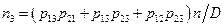 ,
,
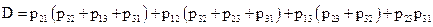 .
.
Формулы (10.13) позволяют найти распределение числа частиц по энергетическим уровням в стационарном состоянии в общем случае присутствия внешней радиации  (
(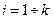 ,
,  ) во всех каналах. Однако большее практическое значение имеет случай нахождения распределения частиц по энергетическим уровням под действием внешнего излучения в канале
) во всех каналах. Однако большее практическое значение имеет случай нахождения распределения частиц по энергетическим уровням под действием внешнего излучения в канале  (с нижнего уровня на верхний). В этом случае населенности уровней являются функциями плотности радиации
(с нижнего уровня на верхний). В этом случае населенности уровней являются функциями плотности радиации  . Определители D и
. Определители D и  (
( ) системы уравнений (10.13) линейно зависят от
) системы уравнений (10.13) линейно зависят от  и могут быть представлены в виде
и могут быть представлены в виде
 ,
,
 , (10.14)
, (10.14)
где  ,
,  ,
, 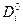 - значения определителей при отсутствии радиации (
- значения определителей при отсутствии радиации ( =0),
=0),  ,
, 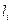 - постоянные коэффициенты.
- постоянные коэффициенты.
Следовательно, населенности энергетических уровней в стационарном режиме определяются выражениями:
 (10.15)
(10.15)
где 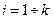 ,
,  – населенность i -го энергетического уровня в отсутствии внешней радиации в канале
– населенность i -го энергетического уровня в отсутствии внешней радиации в канале  ,
,  – параметр нелинейности, характеризующий нелинейность зависимости
– параметр нелинейности, характеризующий нелинейность зависимости  от
от  ; параметр
; параметр  всегда положителен и удовлетворяет соотношению
всегда положителен и удовлетворяет соотношению  (справедливо и более общее соотношение
(справедливо и более общее соотношение  ). В частности, если внешняя радиация частоты
). В частности, если внешняя радиация частоты  индуцирует переходы только между одной парой уровней
индуцирует переходы только между одной парой уровней  , то определители 𝐷 зависят линейно от
, то определители 𝐷 зависят линейно от  , т.е.:
, т.е.:
 ,
,  ,
,  ,
,
Поэтому с учетом (10.15) для числа частиц на уровнях i и j в стационарном состоянии получаем:

 (10.16)
(10.16)
Здесь коэффициенты  и
и  связаны соотношением:
связаны соотношением: 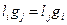 .
. 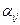 - параметр нелинейности, имеющий размерность [м3Дж-1с-1].
- параметр нелинейности, имеющий размерность [м3Дж-1с-1].
 2020-06-29
2020-06-29 173
173








