Применение определенного интеграла к вычислению площадей плоских фигур

1) Пусть на отрезке  задана непрерывная и неотрицательная функция . Фигура, ограниченная сверху графиком функции , снизу – осью , слева и справа – прямыми  и , называется криволинейной трапецией. Ее площадь  находится по формуле

.

2) Если криволинейная трапеция расположена ниже оси  (функция  неположительна), то ее площадь  находится по формуле

.

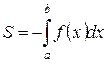3) Если плоская фигура имеет сложную форму, то точками следует разбить отрезок  на части так, чтобы можно было применить уже известные формулы.

.

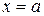4) Площадь фигуры, ограниченной снизу и сверху непрерывными кривыми  и , слева и справа – прямыми  и , можно найти по формуле

.

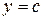5) Площадь криволинейной трапеции, ограниченной непрерывной кривой  (), осью , прямыми  и , находится по формуле

.