Пусть функция  определена на отрезке
определена на отрезке  . Разобьем этот отрезок на
. Разобьем этот отрезок на 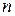 частей точками
частей точками  , на каждом частичном отрезке
, на каждом частичном отрезке  выберем произвольно точку
выберем произвольно точку  и обозначим через
и обозначим через  длину каждого такого отрезка. Интегральной суммой функции
длину каждого такого отрезка. Интегральной суммой функции  на отрезке
на отрезке  называется сумма вида
называется сумма вида
 .
.
Определенным интегралом функции  на отрезке
на отрезке  называется предел интегральной суммы при условии, что длина наибольшего из частичных отрезков стремится к нулю:
называется предел интегральной суммы при условии, что длина наибольшего из частичных отрезков стремится к нулю:
 .
.
Для любой функции  , непрерывной на отрезке
, непрерывной на отрезке  , всегда существует определенный интеграл
, всегда существует определенный интеграл  .
.
Для вычисления определенного интеграла функции  в том случае, когда можно найти соответствующий неопределенный интеграл
в том случае, когда можно найти соответствующий неопределенный интеграл  , служит формула Ньютона-Лейбница:
, служит формула Ньютона-Лейбница:
 ,
,
т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Формула Ньютона-Лейбница связывает определенный и неопределенный интегралы.
Отметим, что определенный интеграл равен числу, в отличие от неопределенного интеграла, представляющего собой семейство функций.
Свойства определенных интегралов:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ,
,  .
.
Пример 1.1. Вычислить следующие определенные интегралы, используя формулу Ньютона - Лейбница:
1)  ;
;
2)  ;
;
3) 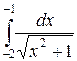 ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9) 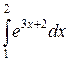 ;
;
10) 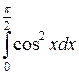 .
.
Решение. 1) Используя формулу  таблицы неопределенных интегралов, получим:
таблицы неопределенных интегралов, получим:
 .
.
2) Переведём корень в степень и используем формулу примера 1).
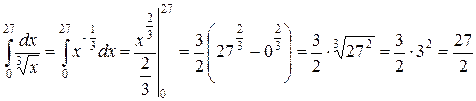 .
.
3) Используя формулу  таблицы неопределенных интегралов, а также, свойство логарифмов
таблицы неопределенных интегралов, а также, свойство логарифмов  , получим:
, получим:
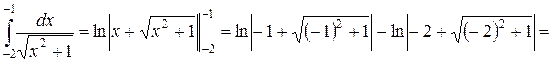
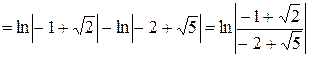 .
.
4) Раскрывая скобки и используя формулу примера 1), получим:
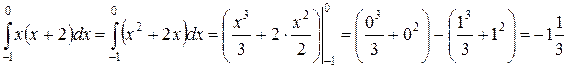 .
.
5) Возведем выражение в квадрат, приведем подобные слагаемые, воспользуемся формулой  и формулой примера 1).
и формулой примера 1).
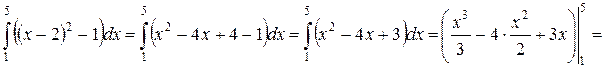

 .
.
6) Разделим почленно числитель на знаменатель, переведем один из корней в степень, воспользуемся формулой 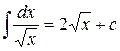 и формулой примера 1).
и формулой примера 1).


 .
.
7) Выделим полный квадрат в знаменателе и воспользуемся формулой 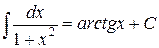 таблицы неопределенных интегралов.
таблицы неопределенных интегралов.
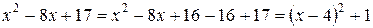 ,
,

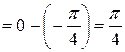 .
.
8) Используя свойство 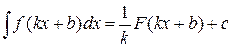 неопределенных интегралов и формулу примера 6), получим:
неопределенных интегралов и формулу примера 6), получим:

 .
.
9) Используя свойство примера 8) и формулу  таблицы неопределенных интегралов, получим:
таблицы неопределенных интегралов, получим:
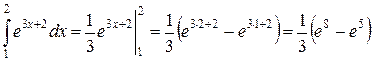 .
.
10) Используя тригонометрическую формулу  и формулу
и формулу  таблицы неопределенных интегралов, получим:
таблицы неопределенных интегралов, получим:
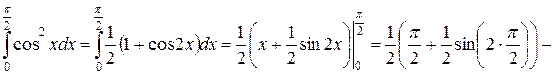
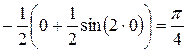 .
.
 2020-06-29
2020-06-29 131
131







