2020-06-29
2230
При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл 
преобразуется с помощью подстановки 
в определенный интеграл относительно новой переменной 
. При этом старые пределы интегрирования 
и 
заменяются соответственно новыми пределами интегрирования 
и 
, которые находятся из равенств 
и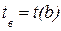 
.
Таким образом, имеем
.
Отличие от замены переменной в неопределенном интеграле состоит в том, что получив искомую первообразную, не нужно возвращаться к старой переменной.
Пример 2.1. Вычислить следующие определенные интегралы, используя метод замены переменной:
1) 
;
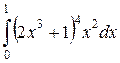2) 
;
3) 
.
Решение. 1) За принимаем самую сложную функцию; если стоит степень – основание степени, если стоит корень – подкоренное выражение.
.
2) При вычислении используем свойство 2) определенных интегралов.
.
3) 
.
Интегрирование по частям в определенном интеграле
Если функции 
и 
и их производные 
и 
непрерывны на отрезке 
, то формула интегрирования по частям для определенного интеграла имеет вид
.
Пример 3.1. Вычислить следующие определенные интегралы, используя метод интегрирования по частям:
1) 
;
2) 
;
3) 
;
4) 
.
Решение. 1) Если подынтегральная функция содержит в виде множителя одну из функций 
, 
, 
, 
, 
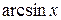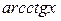, то в качестве функции 
выбирается эта функция.
.
2) Если подынтегральная функция имеет вид 
, 
, 
, где 
- многочлен переменной 
, то в качестве функции выбирается 
, тем самым понижается степень многочлена в новом интеграле.
.
3) Формула интегрирования по частям может использоваться несколько раз.
.
4) Кроме метода интегрирования по частям в примере может применяться и метод замены переменной.
.
