Составление векторных уравнений для группы 2класса2вида

В данной группе Ассура векторные уравнения составляются для точки, являющейся внутренней парой группы – это точка В. Уравнения составляются для звеньев:

· Шатуна АВ;

· ползуна Д.

· Звено АВ совершает плоскопараллельное движение и у него известна скорость точки А - 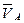, поэтому составим векторное уравнение для скорости точки В по формуле:

(2);

· Ползун В совершает поступательное прямолинейное движение и известна скорость направляющей ползуна – скорость стойки , поэтому составим векторное уравнение для скорости точки В по формуле:

(3);

Чтобы получить необходимо решить графически уравнения (2) и (3) совместно.

Графическое решение уравнений для группы 2класса 2вида.

3. Решение уравнения (2) начинаем от точки а плана скоростей, согласно правилу сложения скоростей – правилу многоугольника. Из (∙) а откладываем 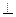АВ – это направление скорости

4. Решение уравнения (3) начинаем из точки Р_V, т.к. скорость . Из точки Р_V откладываем линию параллельную направляющей ползуна, т.к. (рис.11).

5. На пересечении перпендикуляра к звену АВ и линии параллельной направляющей ползуна находится точка b плана скоростей, а отрезок (Р_Vb) - есть изображение скорости .

Определение абсолютных скоростей точек механизма.

Абсолютные скорости точек на плане скоростей изображаются отрезками между точкой полюса Р_V и соответствующей буквой плана скоростей, например, Р_Vа, Р_Vb, и т.д.

Действительные величины абсолютных скоростей определяются с помощью масштабного коэффициента скоростей по формулам: