Этот метод ориентирован на произвольную игру G(m,n)

Не требует условия a_ij>0.

 

 

Рассмотрим метод на примере игры G(3,3).

 

	B1	B2	B3
A1	7	2	9
A2	2	9	0
A3	9	0	11

 

S_A=(p₁,p₂,p₃)

S_B=(q₁,q₂,q₃)

 

 

Строится следующая матрица:

 

k	i	B1	B2	B3	j	A1	A2	A3	V	V	V*
1	3	9	0	11	2	2	9	0	0	9	4.5
2	2	11	9	11	2	4	18	0	4.5	9	6.75
3	2	13	18	11	3	13	18	11	3.67	6	4.84
4	…	…	…	…	…	…	…	…	…	…	…

 

где:

k            – номер партии

i             – номер стратегии, выбираемой игроком A

j             – номер стратегии, выбираемой игроком В

B_i                  – накопленный игроком А выигрыш за k партий, при условии,

                 что в данной партии B выбирает стратегию B_i

А_j                  – накопленный игроком В проигрыш за k партий,

                 при условии, что в данной партии A выбирает стратегию А_j.

V            – нижняя оценка игры = min (накопленный выигрыш)/k

V           – верхняя оценка игры = max (накопленный проигрыш)/k

 

Доказано, что

 

V^*=(V +V)/2, V^* à V при k à ¥ и

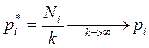
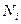- cколько раз выбирается А_i стратегия

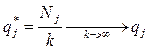
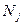 - cколько раз выбирается B_j стратегия

Пример. Задача о двух КБ

 

Объявлен конкурс на выполнение 2-х проектов.

 

На проект 1 выделено а денежных единиц.

На проект 2 выделено b денежных единиц.

 

В конкурсе участвуют 2 КБ:

 

КБ₁(А) – 4 отдела,

КБ₂(В) – 3 отдела.

 

Практика показывает, что если КБ выделяет больше отделов на проект, то оно и получает этот проект, если же они выделяют одинаковое количество отделов, то получения проекта КБ₁ и КБ₂ равновероятны.

 

Стратегии:

 (a,b) - a - количество отделов, выделяемых под первый проект

       b - количество отделов, выделяемых под второй проект

 

 

КБ₁(А):

А₁=(4,0); А₂=(3,1); А₃=(2,2); А₄=(1,3); А₅=(0,4).

КБ₂(В):

В₁=(3,0); В₂=(2,1); В₃=(1,2); В₄=(0,3);

 

Для того, чтобы свести парную игру к антагонистической, вычисляем средний выигрыш – (a+b)/2 и вычитаем его из V.

 

G(5,4):

 

	В1	В2	В3	В4
А1	а/2	(a-b)/2	(a-b)/2	(a-b)/2
А2	b/2	a/2	(a-b)/2	(a-b)/2
А3	(b-a)/2	b/2	a/2	(a-b)/2
А4	(b-a)/2	(b-a)/2	b/2	a/2
А5	(b-a)/2	(b-a)/2	(b-a)/2	b/2

 

 

Пусть а=b.

	В1	В2	В3	В4
А1	a/2	0	0	0
А2	a/2	a/2	0	0
А3	0	a/2	a/2	0
А4	0	0	a/2	a/2
А5	0	0	0	a/2

 

 

	В1	В4
А2	a/2	0
А4	0	a/2

 

S_A=(0,1/2,0,1/2,0)

S_B=(1/2,0,0,1/2)

 

p₁=p₂=1/2

q₁=q₂=1/2

 

V=(a₁₁*p₁+a₂₁*p₂)*q₁+(a₁₂*p₁+a₂₂*p₂)*q₂=a/4

V_КБ1=a/4+a=5a/4

V_КБ2=3a/4

 

Парная игра с произвольной суммой.

(биматричная игра).

 

Аm \Bn В1 … Вn А1       …   || bij||   Аm

Аm \Bn В1 … Вn А1       …   || aij||   Аm

Игра G(m,n)

 

 

Выигрыши игрока А                                     Выигрыши игрока В

Аm \Bn В1 … Вn А1       …   (aij,bij)   Аm

Две данные матрицы объединяют в одну:

 

 

Нет общей теории решения биматричных игр.

В данном классе игр могут быть коалиции, договорённости.

 

Теория некооперативных игр Нэша.

	Аm \Bn В1 … Вn А1       …    (aij,bij)   Аm

 

Необходимо найти решение в виде:

       S_A =(p₁, p₂…, p_N)

       S_B =(q₁, q₂…, q_N)

       Вводится понятие – ситуация равновесия:

       S_A*=(p_i*) i=1..m

       S_B*=(q_j*) j=1..n

                       

Определение.

S_A* и S_B* является ситуацией равновесия, если онаудовлетворяет следующим условиям:

Для игрока А: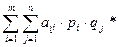

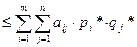
Для игрока В: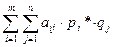

 

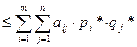
       По Нэшу, решением биматричной игры является ситуация равновесия при условии, что они взаимозаменяемы.

       Нэш доказал, что для любой биматричной игры существует ситуация равновесия, но нет общего метода её поиска.