Приближенные значения приведенного коэффициента сопротивления и приведенной длины для сложных распределительных систем питания определяются из совместного рассмотрения уравнений Д. Бернулли, записанных для каждой ветви. А также уравнений неразрывности и уравнений равенства напоров в узлах.
Галереи, образующие сложную (разветвленную) систему питания, могут быть отнесены к различным порядкам. Тупиковым галереям, которые часто являются распределительными, присваивается первый порядок. Галереи, объединяющие несколько галерей первого порядка, являются галереями второго прядка и т. д. Наивысший порядок будут иметь галереи, получающие питание непосредственно из подводящих галерей, которым порядок не присваивается.
Рассмотрим распределительную систему питания, имеющую два ответвления от подводящей галереи (рис. 2.6, а).
Данная схема имеет две галереи первого порядка (1, 2) и одну подводящую (3).
Полученные величины будем приводить к расчетному сечению подводящей галереи. Уравнения Бернулли для всех ветвей водопроводной системы приобретут вид:
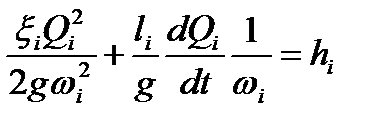 , ,
| (2.23) |
где 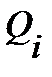 – расход воды, проходящей по i -й ветви;
– расход воды, проходящей по i -й ветви; 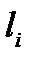 ,
, 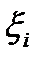 ,
, 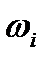 – соответственно длина, коэффициент сопротивления и площадь поперечного сечения i -й ветви; hi – напор на i -й ветви.
– соответственно длина, коэффициент сопротивления и площадь поперечного сечения i -й ветви; hi – напор на i -й ветви.
Во всех ветвях системы питания соблюдается уравнение неразрывности. Исходя из этого, можно записать следующее выражение для определения связи расхода воды в отдельных ветвях водопроводной системы:
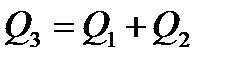 . .
| (2.24) |
Кроме того, в узлах соблюдается равенство напоров:
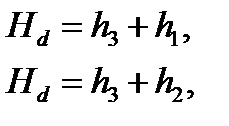
| (2.25) |
где 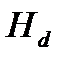 – напор на шлюз.
– напор на шлюз.
Рис. 2.6. Схемы для определения приведенной длины и приведенного коэффициента сопротивления водопроводной системы
Для рассматриваемого случая, используя уравнения (2.23) – (2.25), получим соотношения:
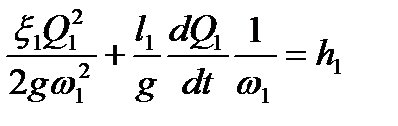 , ,
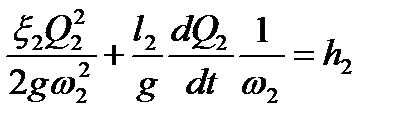 , ,
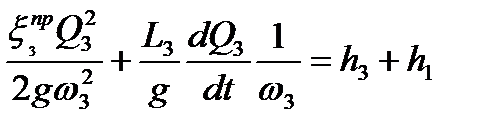 , ,
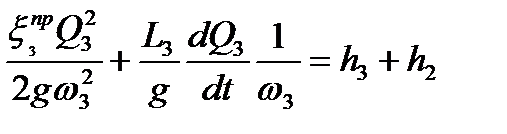 , ,
| (4.26) |
где 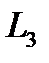 – длина водопроводной системы, приведенная к площади расчетного сечения третьей галереи;
– длина водопроводной системы, приведенная к площади расчетного сечения третьей галереи; 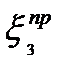 – коэффициент сопротивления водопроводной системы, приведенный к площади расчетного сечения третьей галереи.
– коэффициент сопротивления водопроводной системы, приведенный к площади расчетного сечения третьей галереи.
Уравнения Бернулли для рассматриваемой системы можно записать следующим образом:
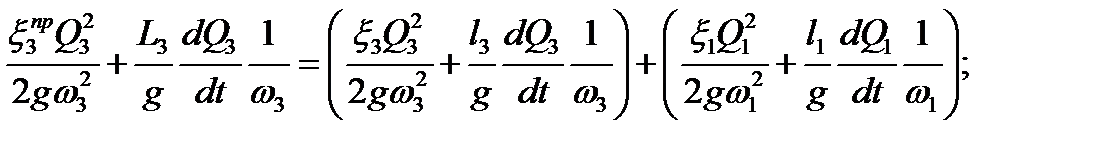 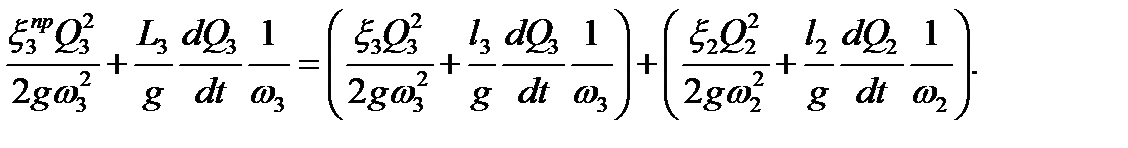
| (2.27) |
Исключив из уравнений (2.27) члены, учитывающие сопротивления движению воды, имеем:
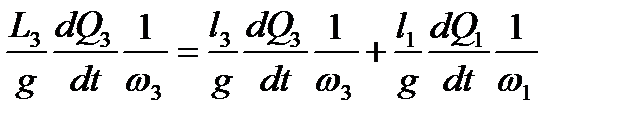 ; ;
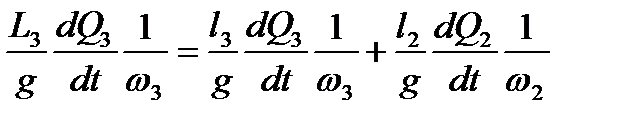 . .
| (2.28) |
Умножив все члены равенств (2.28) на 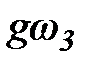 , получим:
, получим:
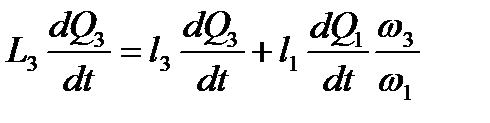 ; ;
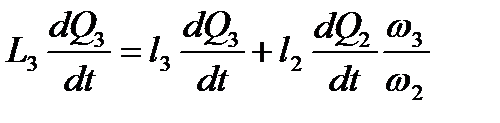 . .
| (2.29) |
Из уравнений (2.29) имеем следующие соотношения:
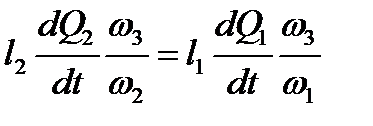 , или , или 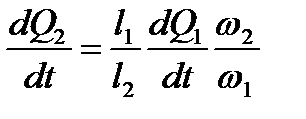 . .
| (2.30) |
Используя (2.30), после ряда преобразований получим уравнение для определения приведенной длины 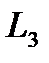 :
:

| (2.31) |
При количестве разветвлений равном n (рис. 2.6, б) приведенная длина водопроводных галерей системы питания определяется по зависимости:
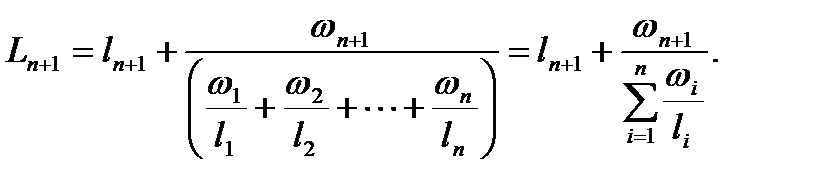
| (2.32) |
Для системы питания, имеющей в своем составе галереи более высоких порядков (несколько разветвлений), приведение длин галерей следует производить последовательно. В первую очередь, приводятся длины галерей первого порядка к площади расчетного сечения галереи второго порядка. Далее длины галерей второго порядка приводятся к площади расчетного сечения галереи третьего порядка и т. д. Окончательное приведение выполняется для подающих галерей.
Поясним алгоритм расчета на примере сложной распределительной системы питания, расчетная схема которой показана на рис. 2.6, в.
Представленный на схеме фрагмент водопроводной системы имеет четыре галереи первого порядка (1 – 4),две галереи второго порядка (5, 6) и одну подводящую (7).
Приведения осуществляется к расчетному сечению подводящей галереи 7. Используя уравнение неразрывности, получаем:
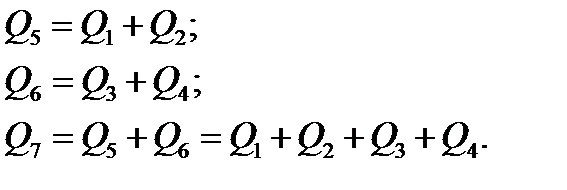
| (2.33) |
Из условия равенства напоров в узлах имеем:
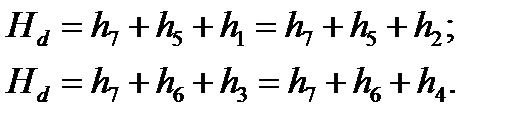
| (2.34) |
Аналогично рассмотренному ранее примеру для галерей первого и второго порядков запишем выражение суммарной длины, приведенной к расчетному сечению галереи второго порядка:
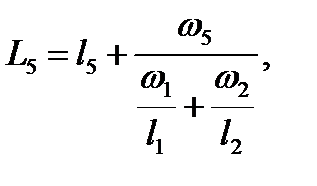
| (2.35) |
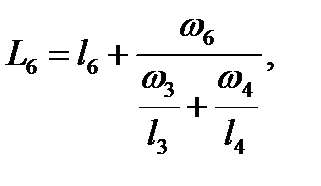
| (2.36) |
где 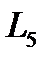 и
и 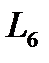 – суммарная длина галерей первого и второго порядков, приведенная к площади расчетного сечения соответственно 5 и 6 галерей.
– суммарная длина галерей первого и второго порядков, приведенная к площади расчетного сечения соответственно 5 и 6 галерей.
Полная длина системы питания 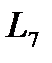 , отнесенная к площади расчетного сечения подводящей галереи, определяется из уравнения:
, отнесенная к площади расчетного сечения подводящей галереи, определяется из уравнения:
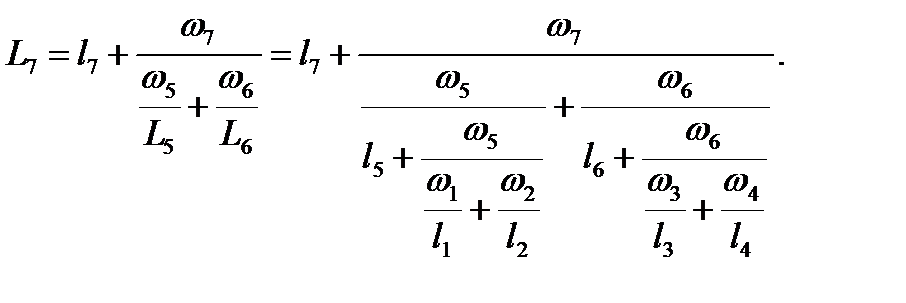
| (2.37) |
Для эквиинерционных систем выражение (2.37) значительно упрощается, так как выполняются соотношения 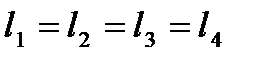 ,
, 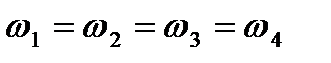 ,
, 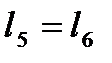 ,
, 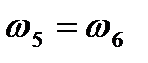 :
:
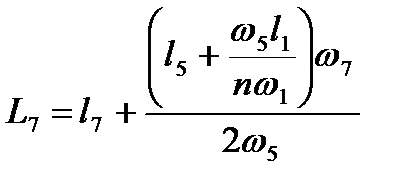 . .
| (2.38) |
Если галереи первого порядка являются распределительными (т.е. с выпусками), то необходимо привести длину галереи и выпусков к ее расчетному сечению.
 2020-06-29
2020-06-29 164
164








