2020-06-29
151
сопротивления сложной распределительной системы
питания
Рассмотрим распределительную систему питания, имеющую два ответвления от подводящей галереи (рис. 2.6, а). В выбранной схеме имеются две галереи первого порядка (1, 2) и одна подводящая (3).
Для всех ветвей системы записываются уравнения Бернулли (2.23), неразрывности (2.24) и равенства напоров (2.25).
Коэффициент сопротивления всей системы, приведенный к площади расчетного сечения подводящей галереи, определяется без учета сил инерции. При такой постановке задачи уравнения (2.27) примут вид:
 ;
 .
| (2.48) |
Умножив (2.48) на 
, получим выражения для 
:
 ;
| (2.49) |
 .
|
Из уравнений (2.49) следует, что:
 , или  .
| (2.50) |
После подстановки (2.50) в уравнение (2.48) и ряда преобразований получим:
 .
| (2.51) |
При проектировании подобных систем, как правило, задаются условием 
. В этом случае уравнение (2.51) примет вид:
 .
| (2.52) |
При количестве разветвлений, равном n (рис. 2.6, б), приведенный коэффициент сопротивления галерей определяется по формуле:
 .
| (2.53) |
При выполнении условий 
, 
, 
и 
уравнение (2.53) будет иметь вид:
 .
| (2.54) |
Для систем питания, имеющих в своем составе галереи более высоких порядков, приведение коэффициентов сопротивлений галерей следует осуществлять последовательно.
В первую очередь, приводят коэффициенты сопротивлений галерей первого порядка к площади расчетного сечения галереи второго порядка. Далее коэффициенты сопротивлений галерей второго порядка приводят к площади расчетного сечения галереи третьего порядка и т. д.
Окончательное приведение выполняется к подающим галереям.
Например (рис. 2.6, в), водопроводная система имеет четыре галереи первого порядка (1 - 4),две галереи второго порядка (5, 6) и одну подводящую (7).
Все приведения будем осуществлять к расчетному сечению подводящей галереи.
Для галерей первого и второго порядков можно записать выражение суммарного коэффициента сопротивления, приведенного к расчетному сечению галереи второго порядка:
 ,
| (2.55) |
 ,
|
где 
и 
– коэффициенты сопротивления галерей первого и второго порядков, приведенные к площади расчетного сечения соответственно пятой и шестой галерей.
Коэффициент сопротивления галерей водопроводной системы 
, отнесенный к площади расчетного сечения подводящей галереи (7), определится следующей зависимостью:
| (2.56) |
Для симметричных эквиинерционных систем имеют место равенства 
, 
, 
, 
, 
, 
, 
, 
, т.е. 
, и (4.56) значительно упрощается:
 .
| (2.57) |
Если галереи первого порядка являются распределительными (галереями с выпусками), то необходимо привести коэффициент сопротивления галереи и выпусков к ее расчетному сечению.
Предлагаемые методы определения коэффициентов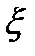 
и длин L являются приближенными, так как при этом не учитываются силы инерции и некоторые сопротивления движению воды в системе питания.
