Понятие первообразной и неопределенного интеграла.
Свойства. Формулы интегрирования.
Первообразная
Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.
Дифференцируемая функция 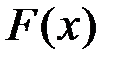 называется первообразной для функции
называется первообразной для функции 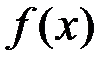 на заданном промежутке, если для всех х из этого промежутка справедливо равенство
на заданном промежутке, если для всех х из этого промежутка справедливо равенство 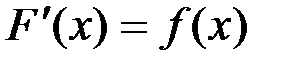 .
.
Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной.
Так, функция 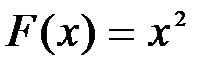 есть первообразная функции
есть первообразная функции 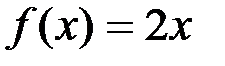 на интервале
на интервале 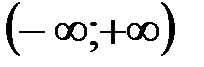 , поскольку для всех
, поскольку для всех 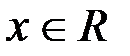 имеет место равенство
имеет место равенство 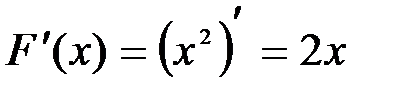 .
.
1. Найти первообразную функции 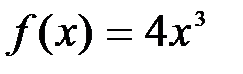 .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале 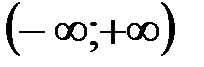 первообразной является первообразной является 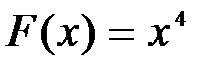 . Действительно, . Действительно, 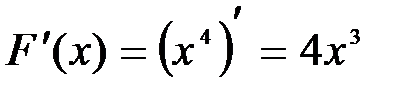 для всех для всех 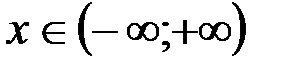 .
2. Найти первообразную функции .
2. Найти первообразную функции 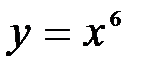 на множестве R.
Решение: Степень на множестве R.
Решение: Степень 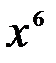 получается при дифференцировании получается при дифференцировании 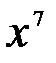 . Так как . Так как 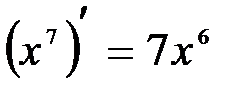 , то, чтобы при дифференцировании , то, чтобы при дифференцировании 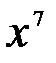 получить перед получить перед 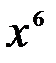 коэффициент 1, нужно коэффициент 1, нужно 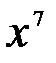 взять с коэффициентом 1/7. Следовательно, взять с коэффициентом 1/7. Следовательно, 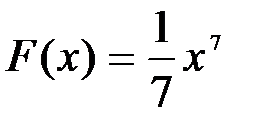 . .
|
Дифференцирование функции – однозначная операция, т.е. если функция имеет производную, то только одну. Это утверждение непосредственно следует из определений предела и производной: если функция имеет предел, то только один. Обратная операция – отыскание первообразной – не однозначна.
Так, функции 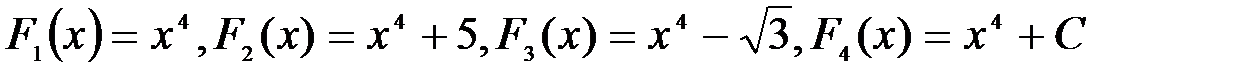 , где С – любое постоянное действительное число, являются первообразными функции
, где С – любое постоянное действительное число, являются первообразными функции 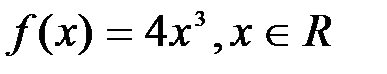 , поскольку все эти функции имеют одну и ту же производную
, поскольку все эти функции имеют одну и ту же производную 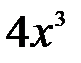 .
.
Теорема. Если 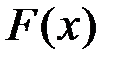 является первообразной функции
является первообразной функции 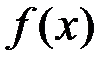 на некотором промежутке, то множество всех первообразных этой функции имеет вид
на некотором промежутке, то множество всех первообразных этой функции имеет вид 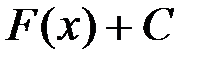 , где С – любое действительное число.
, где С – любое действительное число.
Доказательство: Пусть 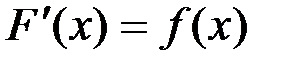 . Тогда
. Тогда 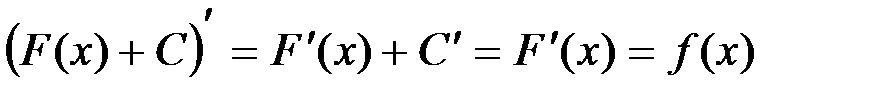 .
.
Покажем теперь, что все первообразные функции 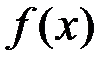 отличаются лишь постоянным слагаемым.
отличаются лишь постоянным слагаемым.
Пусть Ф(х) – другая первообразная функции 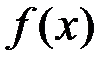 на рассматриваемом промежутке, т.е.
на рассматриваемом промежутке, т.е. 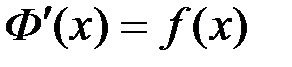 .
.
Тогда 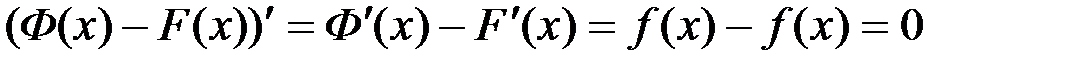 при всех х из рассматриваемого промежутка. Следовательно,
при всех х из рассматриваемого промежутка. Следовательно, 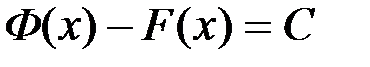 , что и требовалось установить.
, что и требовалось установить.
Таким образом, любые две первообразные данной функции отличаются друг от друга на постоянное слагаемое, а выражение 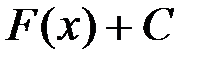 исчерпывает множество всех первообразных заданной функции
исчерпывает множество всех первообразных заданной функции 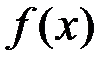 . Итак, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений.
. Итак, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений.
Геометрически выражение 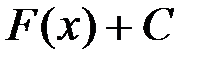 представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси Оу.
представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси Оу.
Неопределенный интеграл
Как уже было отмечено, первообразную можно находить не только по данной ее производной, но и по ее дифференциалу. В дальнейшее мы будем этим пользоваться.
Определение. Совокупность всех первообразных 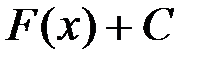 функции
функции 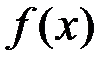 на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом
на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом 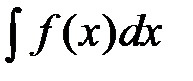 , где
, где 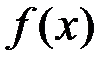 - подынтегральная функция,
- подынтегральная функция, 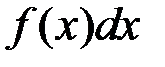 - подынтегральное выражение, х – переменная интегрирования.
- подынтегральное выражение, х – переменная интегрирования.
Таким образом, если 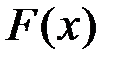 - какая-нибудь первообразная функции
- какая-нибудь первообразная функции 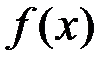 на некотором промежутке, то
на некотором промежутке, то 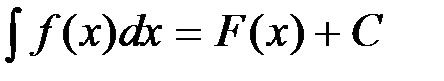 , где С – любое действительное число.
, где С – любое действительное число.
Замечание. Наличие постоянной С делает задачу нахождения функции по ее производной не вполне определенной; отсюда происходит название «Неопределенный интеграл».
Так, пользуясь определением неопределенного интеграла, можно записать: 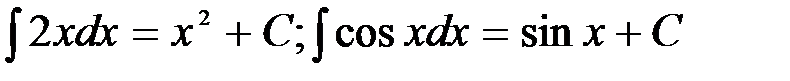 .
.
Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти какую-нибудь одну из ее первообразных и прибавить к ней произвольную постоянную С.
Слово «интеграл» происходит от латинского слова integer, что означает «восстановленный». Интегрируя какую-либо функцию, например 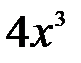 , мы как бы восстанавливаем функцию
, мы как бы восстанавливаем функцию 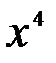 , производная которой равна
, производная которой равна 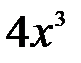 .
.
Чтобы проверить, правильно ли найден неопределенный интеграл, необходимо продифференцировать полученную функцию, если при этом получается подынтегральное выражение, то интеграл найден верно.
Например, 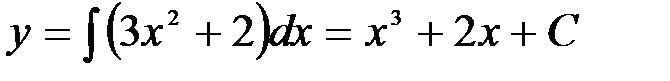 . Сделаем проверку:
. Сделаем проверку: 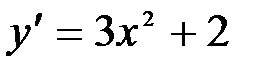 или
или 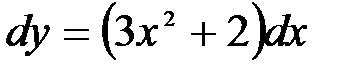 . Следовательно, интеграл найден верно.
. Следовательно, интеграл найден верно.
 2020-06-29
2020-06-29 355
355







