Рассмотрим основные свойства определенного интеграла. При этом мы будем предполагать, что функция 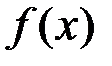 непрерывна на отрезке
непрерывна на отрезке 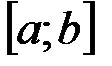 .
.
1. При перестановке пределов интегрирования знак интеграла меняется на противоположный:
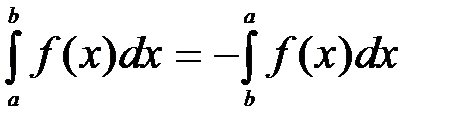 (1).
(1).
Доказательство: Пусть 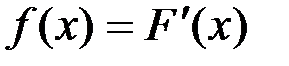 и, значит,
и, значит, 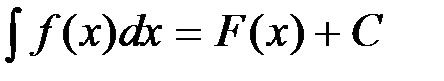 . Тогда
. Тогда 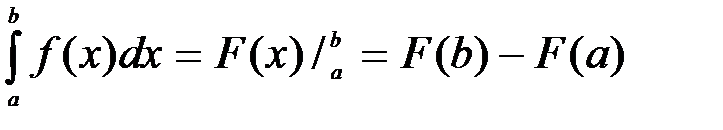 ; (2)
; (2)
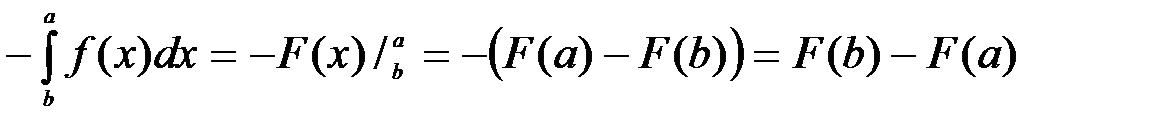 . (3)
. (3)
Правые части равенств (2) и (3) равны; следовательно, должны быть равны и левые части, т.е. справедливо соотношение (1).
Это свойство позволяет рассматривать интегралы, в которых верхний предел меньше нижнего.
2. Постоянный множитель можно вынести за знак определенного интеграла, т.е.
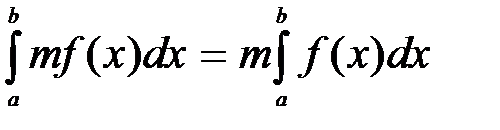 , (4),
, (4),
где m - постоянная величина.
Доказательство: Пусть 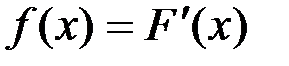 и, следовательно,
и, следовательно, 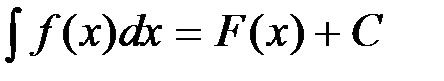 . Тогда
. Тогда 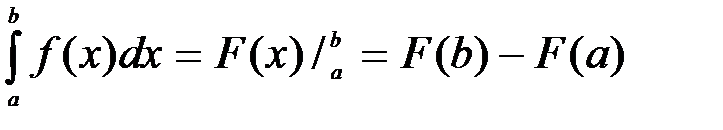 , (5)
, (5)
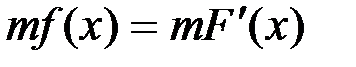 . (6)
. (6)
Из равенства (6) получим 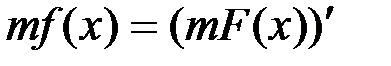 , откуда
, откуда
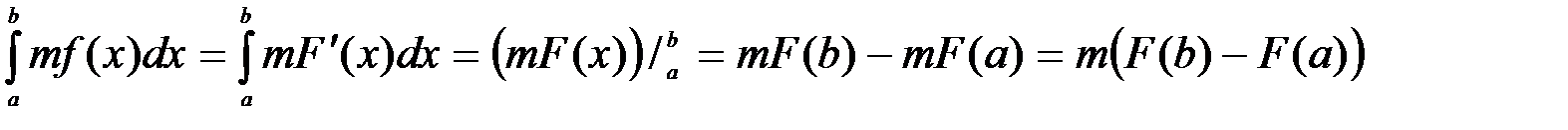 .
.
Но из равенства (5) следует 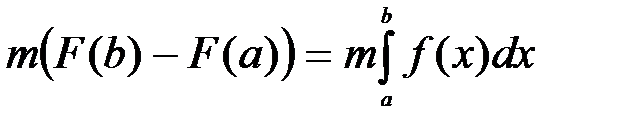 и значит, справедливо соотношение (4).
и значит, справедливо соотношение (4).
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме определенных интегралов от этих функций, т.е.
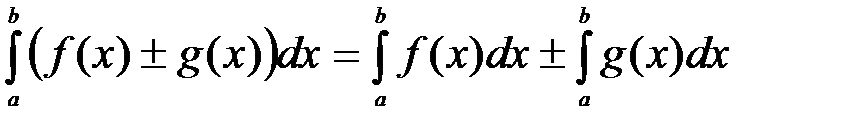 (7)
(7)
Доказательство: Пусть 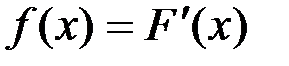 и
и 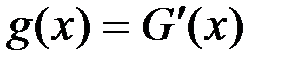 . Тогда
. Тогда 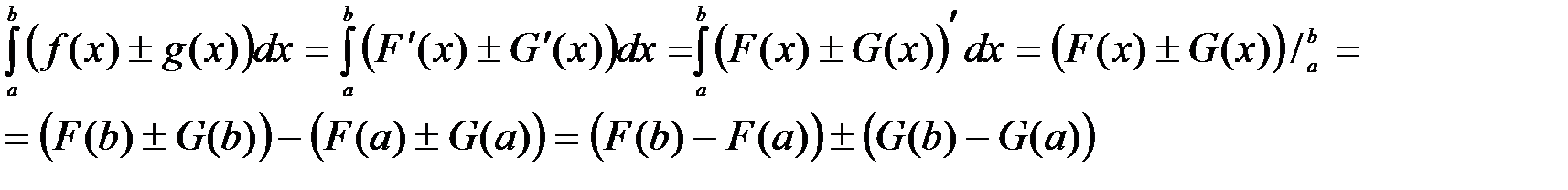
или 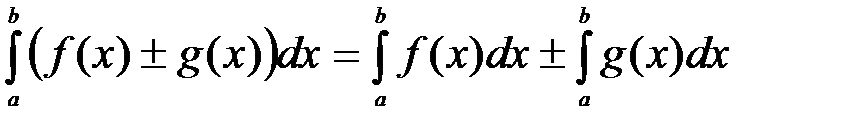 .
.
Аналогично можно доказать справедливость этого свойства для любого конечного числа слагаемых.
4. Если a, b, c принадлежат интервалу, на котором функция 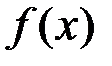 непрерывна, то
непрерывна, то

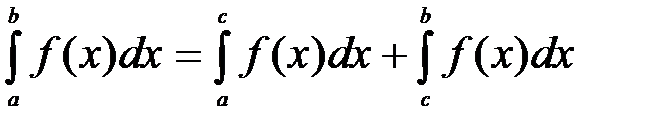 (8).
(8).
Доказательство: Пусть 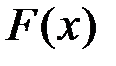 – первообразная функция для
– первообразная функция для 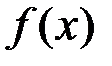 . Тогда
. Тогда
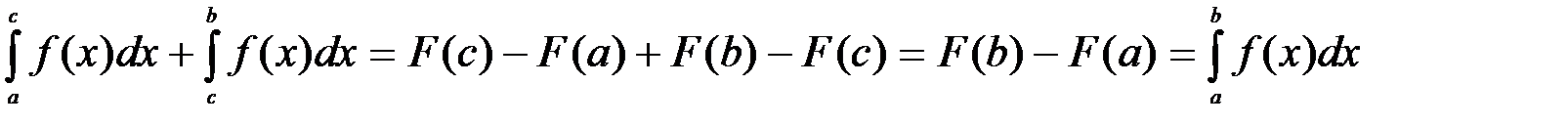 .
.
Вычисление определенного интеграла
1. 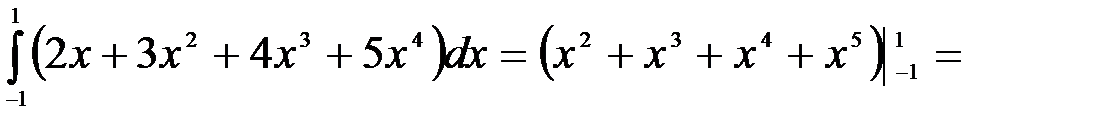
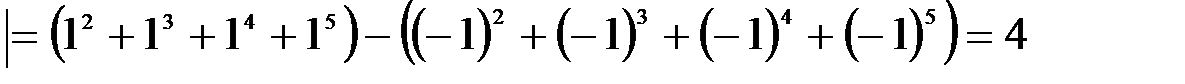
2. 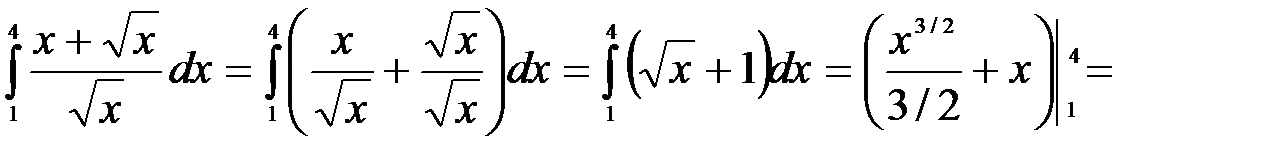
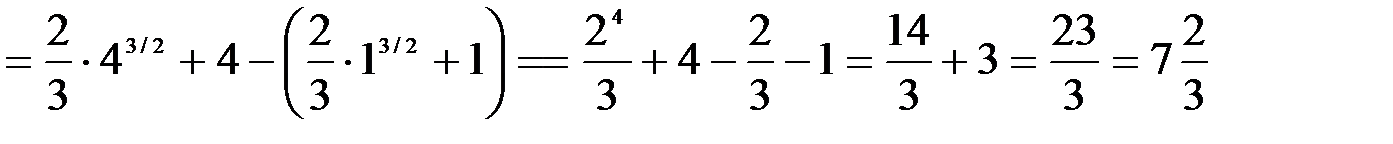
3. 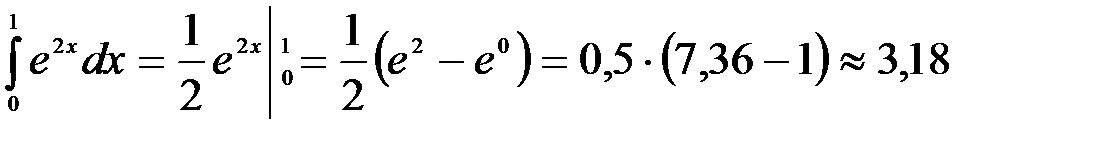
4. 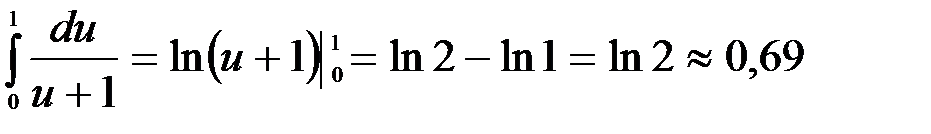
5. 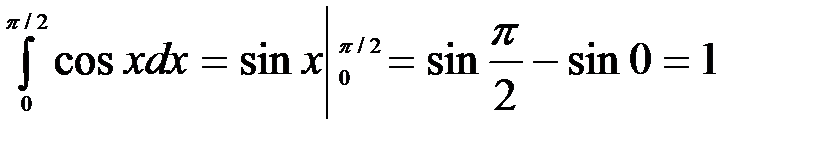
6. 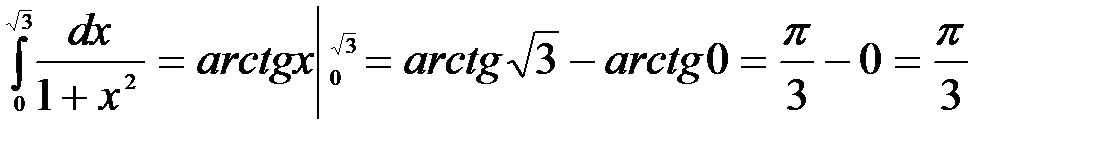
 2020-06-29
2020-06-29 169
169








