Из определения интеграла следует, что для того, чтобы проинтегрировать функцию, нужно найти ее первообразную. Для ряда функций это легко сделать, используя соответствующие формулу интегрирования.
Например, мы знаем, что 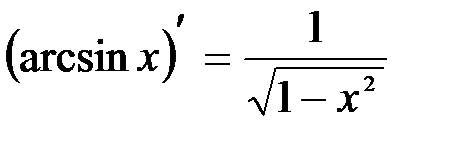 ; отсюда следует, что
; отсюда следует, что 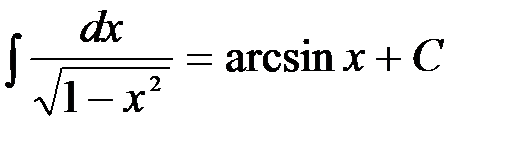 .
.
Итак, формулы интегрирования получаются обращением соответствующих формул дифференцирования. Выпишем в таблицу основные интегралы.
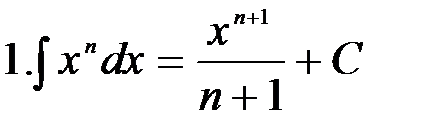 при при 
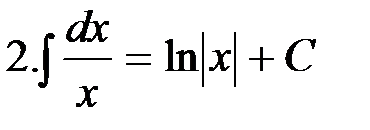
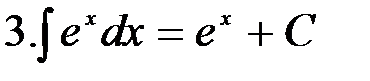
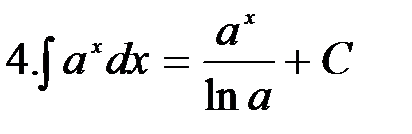
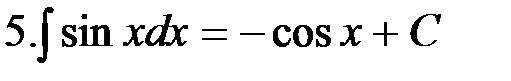
| 

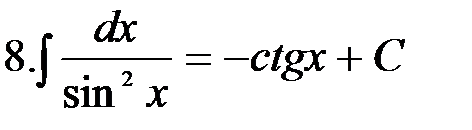
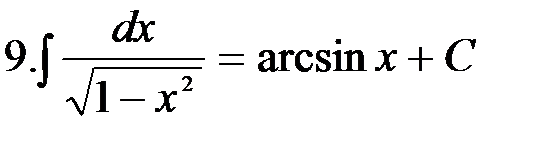

|
Интегралы, приведенные в этой таблице, называются табличными интегралами.
Для вывода этих формул, как уже отмечалось, используется свойство 5 неопределенного интеграла, а именно дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал – подынтегральное выражение.
Формула 1 справедлива при любом n, кроме n=-1, так как в этом случае знаменатель обращается в нуль и выражение теряет смысл. Для доказательства найдем производную правой части равенства:
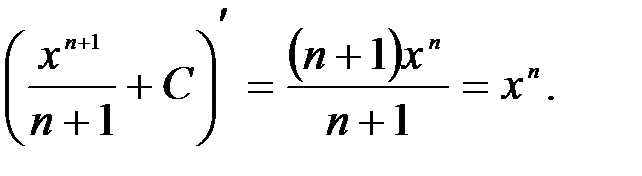
Мы получили подынтегральную функцию; следовательно, формула верна.
Случаю n=-1 соответствует формула 2:

Чтобы найти 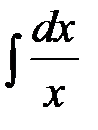 , заметим, что функция
, заметим, что функция  непрерывна в промежутках
непрерывна в промежутках 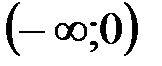 и
и  , причем в каждом из них она имеет первообразную.
, причем в каждом из них она имеет первообразную.
В промежутке 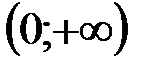 этой первообразной, очевидно, является функция
этой первообразной, очевидно, является функция 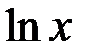 , так как
, так как  , т.е.
, т.е. 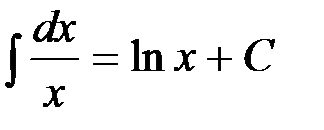 при
при 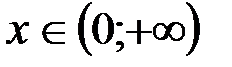 .
.
В промежутке 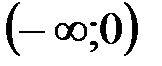 первообразной по отношению к
первообразной по отношению к  является
является 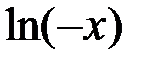 , т.е.
, т.е.  при
при  . Действительно,
. Действительно,  существует при
существует при  и
и 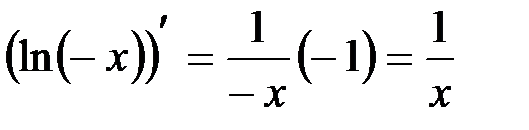 .
.
Итак, оба промежутка непрерывности подынтегральной функции объединяются записью  .
.
Справедливость всех остальных табличных интегралов легко проверить, если продифференцировать их правые части.

Отметим, что формула 3 является частным случаем формулы 4 при  .
.
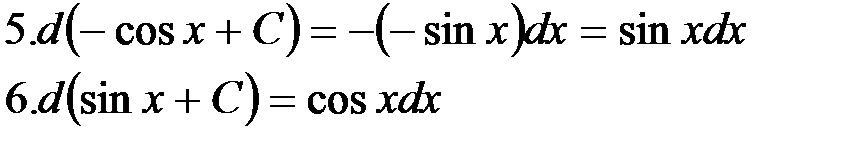
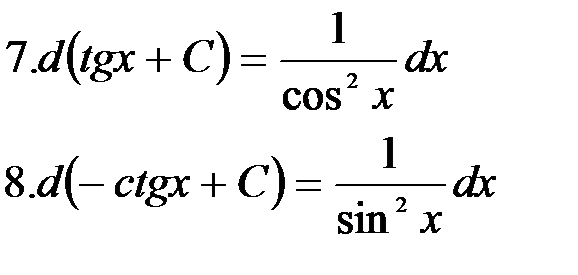

Вычисление интегралов способом приведения их к табличным с помощью преобразования подынтегрального выражения и применения свойств 2 и 3 неопределенного интеграла называется непосредственным интегрированием. При этом полезно запомнить, что  (формула 1 при
(формула 1 при  ).
).
1. 
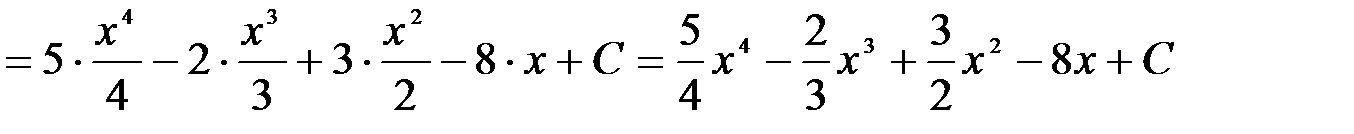
2. 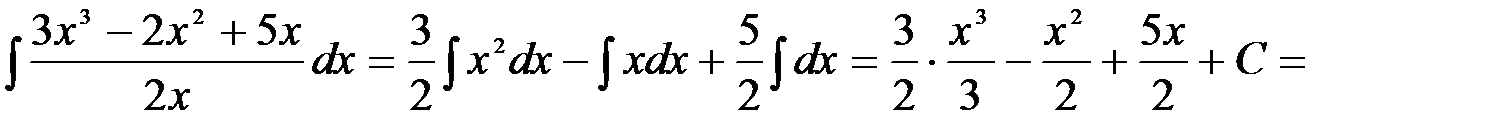
= 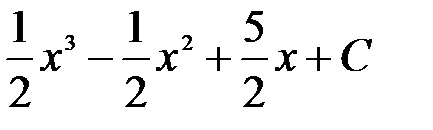
3. 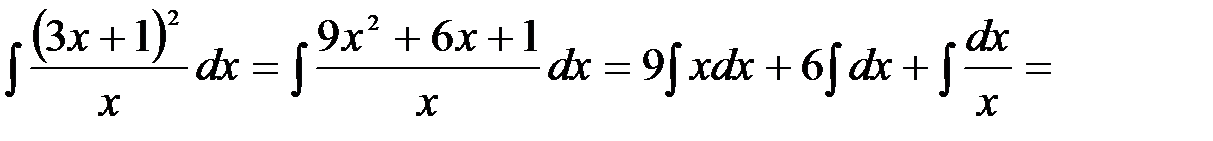
= 
4. 
= 
 2020-06-29
2020-06-29 110
110








