Пусть на отрезке 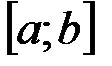 дана непрерывная неотрицательная функция
дана непрерывная неотрицательная функция 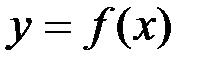 (рис.1). Проведем вертикальные прямые до пересечения с графиком функции
(рис.1). Проведем вертикальные прямые до пересечения с графиком функции 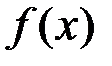 .
.
y
y=f(x)
a b
0 x
рис.1
Определение. Криволинейной трапецией называется фигура, ограниченная графиком непрерывной неотрицательной функции 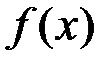 ,
, 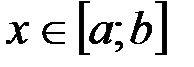 , прямыми
, прямыми 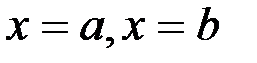 и отрезком оси
и отрезком оси 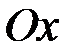 .
.
Как вычислить площадь криволинейной трапеции? Рассмотрим криволинейную трапецию CHKD (рис.2), у которой абсцисса точки С равна х, а абсцисса точки D равна 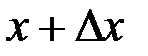 . Пусть график функции
. Пусть график функции 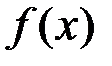 пересекает ось ординат в точке А. Тогда площадь криволинейной трапеции CHKD равна разности площади криволинейной трапеции OAKD и OAHC. Так как площадь криволинейной трапеции OAHC зависит от х, то ее можно обозначить символом S(x). Аналогично, площадь криволинейной трапеции OAKD есть функция от
пересекает ось ординат в точке А. Тогда площадь криволинейной трапеции CHKD равна разности площади криволинейной трапеции OAKD и OAHC. Так как площадь криволинейной трапеции OAHC зависит от х, то ее можно обозначить символом S(x). Аналогично, площадь криволинейной трапеции OAKD есть функция от 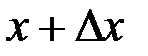 и ее можно обозначить символом S(
и ее можно обозначить символом S(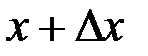 ). Поэтому площадь криволинейной трапеции CHKD равна разности S(
). Поэтому площадь криволинейной трапеции CHKD равна разности S(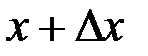 ) и S(x) иможет быть обозначена символом
) и S(x) иможет быть обозначена символом 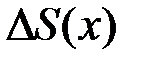 .
.
Построим два прямоугольника CHED и CMKD. Площадь первого из них равна 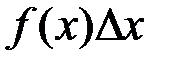 , а площадь второго равна
, а площадь второго равна 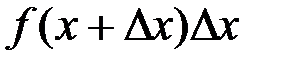 . Поскольку площадь криволинейной трапеции CHKD не меньше площади прямоугольника CHED и не больше площади прямоугольника CMKD, можно записать неравенство.
. Поскольку площадь криволинейной трапеции CHKD не меньше площади прямоугольника CHED и не больше площади прямоугольника CMKD, можно записать неравенство.
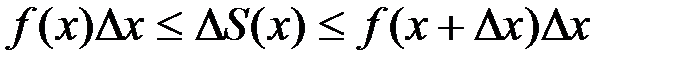
Разделив обе части этого неравенства на 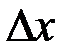 и найдем пределы всех выражений при
и найдем пределы всех выражений при 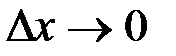 . Но
. Но 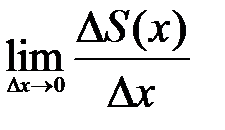 есть производная функции S(x), а в силу непрерывности функции
есть производная функции S(x), а в силу непрерывности функции 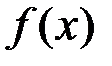 имеем
имеем 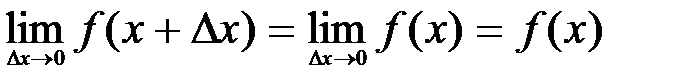 . Следовательно,
. Следовательно, 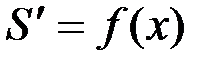 .
.
Итак, производная площади криволинейной трапеции равна функции, задающей верхнюю границу трапеции.
Поэтому площадь криволинейной трапеции есть одна из первообразных функции, задающей верхнюю границу трапеции, и может быть вычислена с помощью интегрирования: 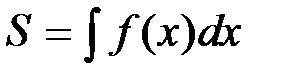
y M K
H E
A f(x) f( 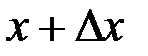 )
)
x 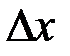
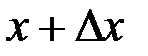
O C D x
рис.2
Пусть 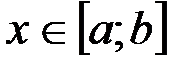 . Площадь криволинейной трапеции, заштрихованной на рис.3, есть функция от х. Обозначим ее через S(x). Очевидно, что S(a)=0, так как при х=а заштрихованная фигура превращается в отрезок, а S(b)=S есть площадь рассматриваемой криволинейной трапеции.
. Площадь криволинейной трапеции, заштрихованной на рис.3, есть функция от х. Обозначим ее через S(x). Очевидно, что S(a)=0, так как при х=а заштрихованная фигура превращается в отрезок, а S(b)=S есть площадь рассматриваемой криволинейной трапеции.
Замечание. Когда говорят о непрерывности функции 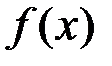 на промежутке
на промежутке 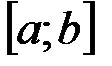 , то под этим понимают непрерывность ее в каждой точке этого промежутка, в том числе в точках a и b, т.е., что
, то под этим понимают непрерывность ее в каждой точке этого промежутка, в том числе в точках a и b, т.е., что 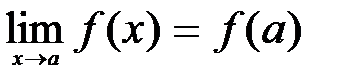 при стремлении х к а и
при стремлении х к а и 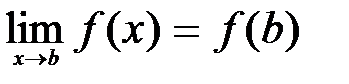 при стремлении х к b.
при стремлении х к b.
Используя равенство 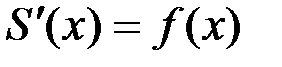 , где
, где 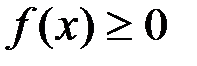 на промежутке
на промежутке 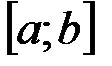 , выведем формулу для вычисления площади криволинейной трапеции (см.рис.3). Из этого равенства видно, что S(x) есть первообразная для
, выведем формулу для вычисления площади криволинейной трапеции (см.рис.3). Из этого равенства видно, что S(x) есть первообразная для 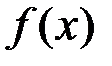 на промежутке
на промежутке 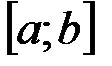 . Пусть
. Пусть 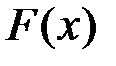 – другая первообразная для
– другая первообразная для 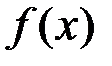 на этом же промежутке. В силу основного свойства первообразной имеем
на этом же промежутке. В силу основного свойства первообразной имеем 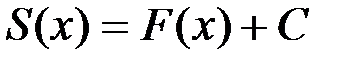 .
.
y
y=f(x)
S(x)
0 a x b x
рис.3
Последнее равенство верно при всех 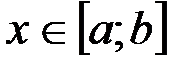 , так как функции S(x) и
, так как функции S(x) и 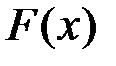 определены в точках a и b. Подставив вместо x число a, получим
определены в точках a и b. Подставив вместо x число a, получим 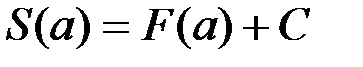 . Но
. Но 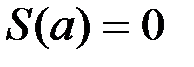 , поэтому
, поэтому 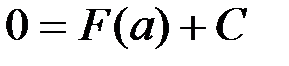 , откуда
, откуда 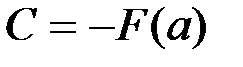 . Таким образом,
. Таким образом, 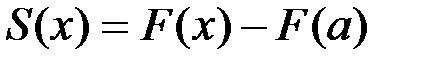 .
.
Подставив в последнее равенство 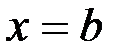 , найдем искомую площадь:
, найдем искомую площадь:
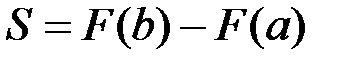 (1)
(1)
Напомним, что приращением аргумента х при его изменении от 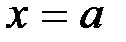 до
до 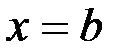 называется разность
называется разность 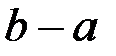 , а приращением функции
, а приращением функции 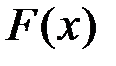 при изменении аргумента от
при изменении аргумента от 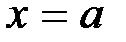 до
до 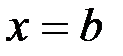 называется разность
называется разность 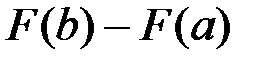 .
.
Найдем приращение любой первообразной функции 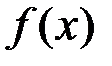 при изменении аргумента от
при изменении аргумента от 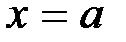 до
до 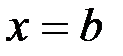 :
:
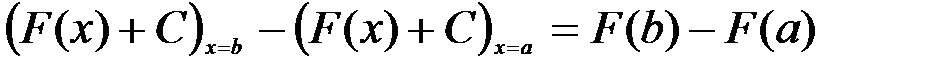
Полученный результат означает, что при изменении х от 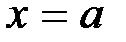 до
до 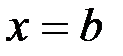 все первообразные для данной функции имеют одно и то же приращение, равное
все первообразные для данной функции имеют одно и то же приращение, равное 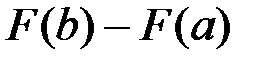 .
.
Это приращение принято называть определенным интегралом.
Определение. Если 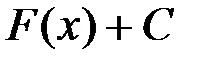 – первообразная функция для
– первообразная функция для 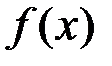 , то приращение
, то приращение 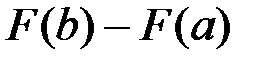 первообразных функций при изменении аргумента х от
первообразных функций при изменении аргумента х от 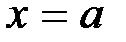 до
до 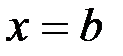 называется определенным интегралом и обозначается символом
называется определенным интегралом и обозначается символом 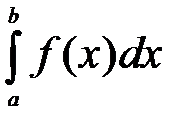 , т.е.
, т.е.
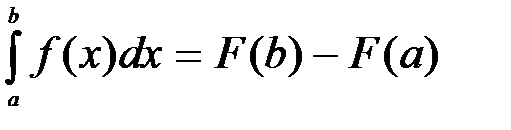 ,
,
где 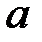 – нижний предел, а
– нижний предел, а 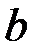 – верхний предел определенного интеграла.
– верхний предел определенного интеграла.
Символ читается так: «определенный интеграл от 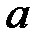 до
до 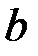 эф от икс дэ икс».
эф от икс дэ икс».
Функция 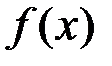 предполагается непрерывной в промежутке изменения аргумента х от
предполагается непрерывной в промежутке изменения аргумента х от 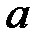 до
до 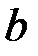 .
.
Для вычисления определенного интеграла 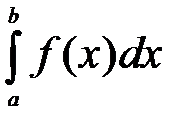 находят:
находят:
1) неопределенный интеграл 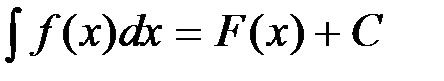 ;
;
2) значение интеграла 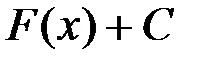 при
при 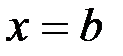 , С=0, т.е. вычисляют
, С=0, т.е. вычисляют 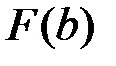 ;
;
3) значение интеграла 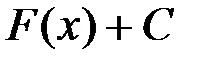 при
при 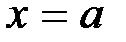 , С=0, т.е. вычисляют
, С=0, т.е. вычисляют 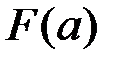 ;
;
4) разность 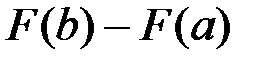 .
.
Процесс вычисления виден из формулы:
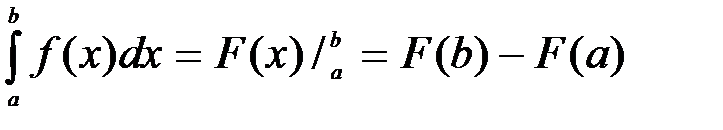 (2)
(2)
 2020-06-29
2020-06-29 199
199








