Основные свойства неопределенного интеграла

Из рассмотренных ранее примеров видно, что можно находить интегралы, подбирая первообразные. Однако это не всегда просто. При интегрировании помогает знание некоторых свойств интеграла, формул интегрирования, а также специальных приемов.

Рассмотрим сначала основные свойства неопределенного интеграла.

 

1. Производная неопределенного интеграла равна подынтегральной функции, т.е.

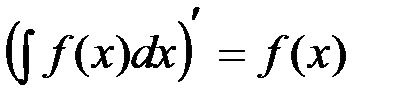
Это свойство непосредственно вытекает из определения неопределенного интеграла, поскольку 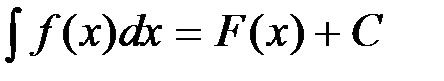, а .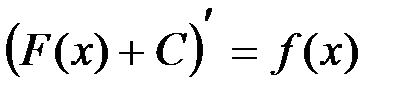

Так, .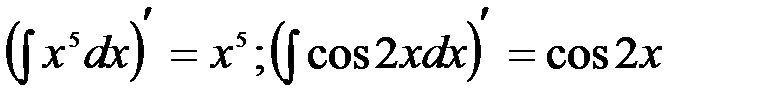

На этом свойстве основано доказательство следующих свойств.

 

1. Постоянный множитель подынтегрального выражения можно вынести за знак интеграла, т.е.

,

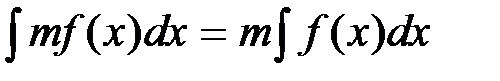 где m – постоянная величина, не равная нулю.

Это свойство доказывается дифференцированием обеих частей приведенного равенства. При этом учитывается свойство 1: производная неопределенного интеграла равна подынтегральной функции.

Действительно,

 .

Например, , где а – постоянная, не равная нулю.

 

1. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций, т.е.

Для доказательства найдем производные обеих частей равенства и покажем, что они равны между собой. Сначала найдем производную левой части:

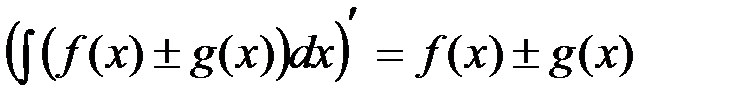
мы воспользовались свойством 1 неопределенного интеграла.

Теперь найдем производную правой части равенства:

.

Здесь был использован тот факт, что производная алгебраической суммы функций равна алгебраической сумме этих функций, а также свойство 1 неопределенного интеграла.

Итак, производные обеих частей равенства равны между собой, что и доказывает свойство 3.

1. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.

.

Это свойство следует из определения неопределенного интеграла. Действительно, 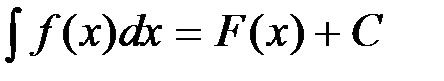, а 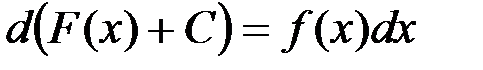. Свойство 4 означает, что знак дифференциала аннулирует знак интеграла.

Например, 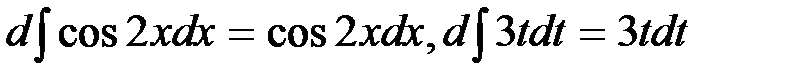 и т.д.

 

1. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С, т.е.

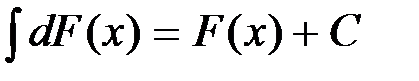 или .

Действительно, 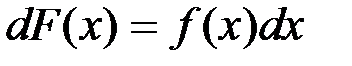. Возьмем интеграл от обеих частей равенства и получим 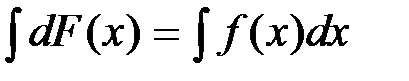. Но, по определению, 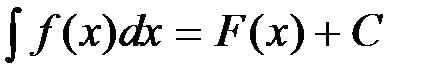, т.е. .

Например, и т.д.

На основании этого свойства выводятся формулы интегрирования.