Криволинейные координаты и радиус вектор, параметризация поверхности

По дисциплине «Математический анализ»

ЭЛЕМЕНТЫ дифференциальнОЙ геометриИ поверхностей

Выполнила:

Швец Екатерина Михайловна,

студентка 2 курса направления подготовки

01.03.02 «Прикладная математика и информатика» очной формы обучения

 

Научный руководитель:

Кацуба Валентина Сергеевна, к.ф.-м.н., доцента, доцент кафедры физики, информатики и ИТ

Мурманск

2018 г.
ОГЛАВЛЕНИЕ

 

ВВЕДЕНИЕ. 3

Глава I. СВЕДЕНИЯ ИЗ ПРЕДМЕТНОЙ ОБЛАСТИ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧИ.. 5

1.1    Криволинейные координаты и радиус вектор, параметризация поверхности. 5

1.2    Длина дуги, первая квадратичная форма. 7

1.3    Вторая квадратичная форма. 8

1.4    Нормальные кривизны, гауссова кривизна. 11

Глава II. ВЫЧИСЛЕНИЕ ХАРАКТЕРНЫХ ВЕЛИЧИН ДЛЯ ПРОСТЫХ ПОВЕРХНОСТЕЙ.. 13

2.1    Сфера. 13

2.2    Цилиндр. 16

2.3    Конус. 18

Глава III. ПРИМЕРЫ НАХОЖДЕНИЯ ХАРАКТЕРНЫХ ВЕЛИЧИН ДЛЯ СЛОЖНЫХ ПОВЕРХНОСТЕЙ.. 21

3.1    Тор. 21

3.2    Геликоид. 24

ЗАКЛЮЧЕНИЕ. 27

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 28

ПРИЛОЖЕНИЯ.. 30

 

ВВЕДЕНИЕ

 

Дифференциальная геометрия поверхностей – это раздел математики, который изучает поверхности методами дифференциальной геометрии. При этом поверхности, которые исследуются, обычно подчинены условиям, связанным существованием в каждой точке поверхности определенных кривизн, внутренних точек и т.д.

Тема «Элементы дифференциальной геометрии поверхностей» уникальна тем, что в настоящее время поверхности играют особую роль в жизни человека. Большинство окружающих нас предметов можно представить в виде поверхностей. Трудно представить себе область науки или производства, где не используют поверхности. Поверхности используются во многих сферах человеческой деятельности: строительстве, судостроении, ракетостроении и т.д. Сложные поверхности представляют собой арки мостов, корпуса кораблей, крыши зданий. Все вышеперечисленное требует знания различных свойств этих поверхностей, чтобы упростить работу с ними и, например, сделать поверхности более крепкими и устойчивыми. Поэтому изучение элементов теории дифференциальной геометрии поверхности является актуальным для профессиональной подготовки по специальности «прикладная математика и информатика».

Основная цель данной курсовой работы состоит в исследовании некоторых свойств поверхностей средствами дифференциальной геометрии. Объектом курсовой работы являются элементы дифференциальной геометрии поверхностей.

Предмет курсовой работы – параметризация поверхностей с помощью внутренних криволинейных координат, первая и вторая квадратичные формы поверхности, нормальная и Гауссова кривизна.

Для достижения цели курсовой работы были решены следующие задачи: проведены поиск, изучение и систематизация основных теоретических фактов, связанных с дифференциальной геометрией поверхности: параметризация поверхностей с помощью внутренних криволинейных координат, первая и вторая квадратичные формы поверхности, средняя и гауссова кривизна; рассмотрены приложения изученных теоретических фактов к следующим поверхностям: сфера, конус, цилиндр, тор, геликоид.

Данная курсовая работа содержит: введение, три главы, заключение, список использованных источников, три приложения.

Глава I. СВЕДЕНИЯ ИЗ ПРЕДМЕТНОЙ ОБЛАСТИ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧИ

 

Криволинейные координаты и радиус вектор, параметризация поверхности

 

Пусть на поверхности задано некоторое семейство линий, зависящих от одного параметра. Семейство называется правильным [5] в некоторой области точек поверхности, если через каждую точку этой области проходит одна и только одна линия семейства.

Если на поверхности заданы два семейства линий, то они образуют сеть в той области, в которой оба семейства правильны, причем в этой области линии различных семейств пересекаются только в одной точке, не совпадают между собою и не касаются друг друга.

Пусть на поверхности задана сеть, удовлетворяющая всем этим условиям (см. рис.1). Линия одного семейства этой сети определяется значением параметра u, а линия другого семейства значением параметра v.

Рисунок 1 – Сеть на поверхности

 

Положение точки определит задание этих параметров, соответствующих кривым, пересекающимся в точке области. Так как через каждую точку области проходят определенные линии каждого семейства, то всякой фиксированной точке соответствуют определенные значения параметров u и v.

Криволинейные координаты [8] точки – это значения параметров u и v, определяющих кривые сети и пересекающиеся в данной точке поверхности. Эти линии и образованная ими сеть называются координатными линиями и координатной сетью. Вдоль одной координатной линии изменяется только одна криволинейная координата, а другая остается постоянной. На рисунке 2 приведен пример криволинейных координат на поверхности сферы.

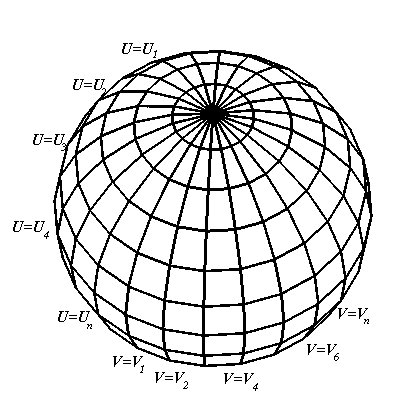
Рисунок 2 – Криволинейные координаты сферы

 

Если на поверхности введены криволинейные координаты, то говорят, что поверхность параметризована. Параметризация является наиболее удобным заданием поверхности. Задать поверхность параметризацией – значит задать поверхность, как график двумерной вектор-функции. Обозначим через 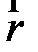 радиус-вектор точки на поверхности, он определяется независимыми u, v, функция  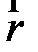является функцией двух скалярных аргументов (u,v), т.е. .

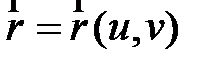Пусть поверхность задана параметрическим уравнением 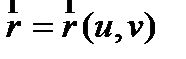, а принадлежащая ей кривая параметризована [2] с помощью параметра t. Таким образом, криволинейные координаты точек кривой, расположенных на поверхности являются функциями от t, т.е. каждому t соответствует (u,v)

(). Параметризация кривой в трехмерном пространстве будет выглядеть следующим образом:

   (1)

Например, поверхности вращения [10] задаются следующим образом: пусть дана кривая, которая задана в плоскости xoz и будет вращаться вокруг оси oz:

                                                  (2)

Тогда поверхность будет задана:

                                (3)