Глава III. Примеры нахождения характерных величин для сложных поверхностей

 

Тор

 

Тор – поверхность, которая получается при вращении окружности  вокруг оси oz. Тогда используя формулу (2) и (3) получим параметризацию сферы (см. рис.6):

Рисунок 6 – Криволинейные координаты тора

 

Найдем координатные векторы и по формуле (10):

Далее найдем коэффициенты E, F, G первой квадратичной формы:

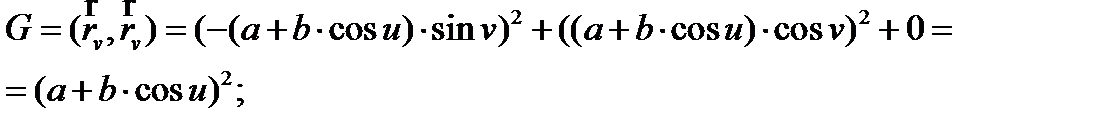
Таким образом, первая квадратичная форма будет выглядеть следующим образом:

Найдем координатные векторы  по формуле (10):

Для нахождения коэффициентов L, M, N второй квадратичной формы необходимо найти единичный вектор нормали :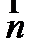

Найдем коэффициенты L, M, N второй квадратичной формы:

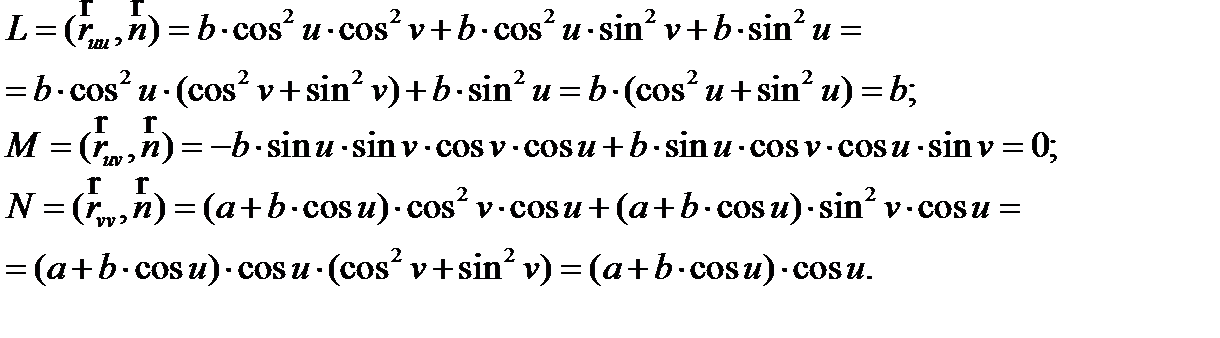
Таким образом, вторая квадратичная форма будет выглядеть следующим образом:

Найдем гауссову кривизну:

Найдем среднюю кривизну:

Таким образом, если сравнить матрицы первых квадратичных форм тора –  и сферы – , можно сделать вывод, что при a =0, матрица тора вырождается в матрицу сферы, т.е. сфера является частным случаем тора.

Геликоид

 

Геликоид – поверхность, образованная движением прямой, вращающейся вокруг оси и перпендикулярной к ней и одновременно поступательно движущейся в направлении этой оси, причем скорости этих движений пропорциональны. Параметризация Геликоида выглядит следующим образом (см. рис.7):

 

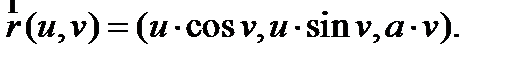
Рисунок 7 – Криволинейные координаты геликоида

 

Найдем координатные векторы и по формуле (10):

Далее найдем коэффициенты E, F, G первой квадратичной формы:

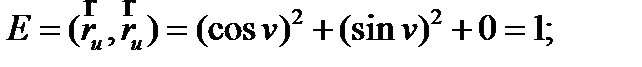
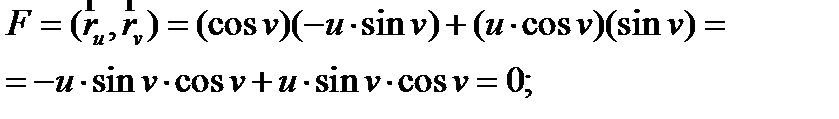
Таким образом, первая квадратичная форма будет выглядеть следующим образом:

Найдем координатные векторы  по формуле (10):

Для нахождения коэффициентов L, M, N второй квадратичной формы необходимо найти единичный вектор нормали :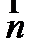

Найдем коэффициенты L, M, N второй квадратичной формы:

Таким образом, вторая квадратичная форма будет выглядеть следующим образом:

 

Найдем среднюю кривизну:

Найдем гауссову кривизну:

В данном случае гауссова кривизна отрицательна (K <0), поэтому поверхность является выпукло-вогнутой, что является верным утверждением по отношению к геликоиду, а средняя кривизна всегда равна 0.

 

ЗАКЛЮЧЕНИЕ

 

Таким образом, в ходе исследования элементов дифференциальной геометрии поверхностей, были выполнены следующие задачи:

· изучены все сведения из предметной области, которые были необходимы для решения задачи;

· проведен подробный анализ простых поверхностей – сферы, цилиндра, конуса; и более сложных – тора и геликоида;

· проведена параметризация поверхностей с помощью внутренних криволинейных координат, были найдены первая и вторая квадратичные формы поверхности, средняя и Гауссова кривизна;

· выявлено, что матрицы первой квадратичной формы сложных и простых поверхностей отличаются только элементами на главной диагонали матрицы, а элементы на побочной диагонали всех поверхностей – равны 0;

· подтверждены свойства гауссовой кривизны на конкретных примерах;

· найдена связь между сложной поверхности – тора, и простой поверхности – сферы, при помощи первой квадратичной формы;

· при работе со всеми формулами использовался математический редактор формул MathType 6;

· разработана программа визуализации поверхностей заданных параметрически, с помощью математической программы MATLAB [11].

Таким образом, цель данной курсовой работы была достигнута. В процессе изучения был получен опыт исследования некоторых характерных величин для поверхностей средствами дифференциальной геометрии.