Для того, чтобы понять кривизну поверхности, наиболее удобным приемом является использование нормальных сечений поверхности. Тогда, нормальные кривизны [7] для нормальных сечений задаются функцией:
 . (20)
. (20)
У функции  есть два экстремальных значения:
есть два экстремальных значения:
 (21)
(21)
где  – главные кривизны поверхности в точке.
– главные кривизны поверхности в точке.
Перемножив главные кривизны формулы (21), получим гауссову кривизну:
 . (22)
. (22)
Гауссова кривизна имеет несколько замечательных свойств [1]:
· Если гауссова кривизна положительная (К>0), то поверхность является двояковыпуклой.
· Если гауссова кривизна нулевой кривизны (К=0), то поверхность является цилиндрической или конической.
· Если гауссова кривизна отрицательна (К<0), то поверхность является выпукло-вогнутой.
· не изменяется при изометрических изгибаниях.
Найдя среднее арифметическое главных кривизн формулы (21), получим среднюю кривизну:
 . (23)
. (23)
Таким образом, основными характерными элементами дифференциальной геометрии поверхностей являются: первая и вторая квадратичные формы поверхности, средняя и гауссова кривизна
Глава II. ВЫЧИСЛЕНИЕ ХАРАКТЕРНЫХ ВЕЛИЧИН ДЛЯ ПРОСТЫХ ПОВЕРХНОСТЕЙ
Сфера
Сфера задана вращением окружности радиуса R в плоскости xoz вокруг оси OZ:  Реализацию программы построения сферы в криволинейных координатах можно увидеть в приложении А.
Реализацию программы построения сферы в криволинейных координатах можно увидеть в приложении А.
Тогда используя формулу (2) и (3) получим параметризацию сферы (см. рис.3):


Рисунок 3 – Криволинейные координаты сферы
Найдем координатные векторы  и
и  по формуле (10):
по формуле (10):

Далее найдем коэффициенты E, F, G первой квадратичной формы:



Таким образом, первая квадратичная форма будет выглядеть следующим образом:

Найдем координатные векторы  по формуле (10):
по формуле (10):

Для нахождения коэффициентов L, M, N второй квадратичной формы необходимо найти единичный вектор нормали 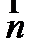 :
:


Найдем коэффициенты L, M, N второй квадратичной формы:

Таким образом, вторая квадратичная форма будет выглядеть следующим образом:

Найдем среднюю кривизну:

Найдем гауссову кривизну:

В данном случае, гауссова кривизна всегда больше 0, поэтому можно сделать вывод по одному из свойств гауссовой кривизны, что поверхность является двояковыпуклой, что является верным утверждением по отношению к сфере.
Цилиндр
Параметризация (см. рис.4) цилиндра с окружностью радиуса а в основании:  Реализацию программы построения цилиндра в криволинейных координатах можно увидеть в приложении B.
Реализацию программы построения цилиндра в криволинейных координатах можно увидеть в приложении B.

Рисунок 4 – Криволинейные координаты цилиндра
Найдем координатные векторы  и
и  по формуле (10):
по формуле (10):

Далее найдем коэффициенты E, F, G первой квадратичной формы:



Таким образом, первая квадратичная форма будет выглядеть следующим образом:

Если выбрать значение а =1, то матрица превратится в единичную. Это указывает на то, что цилиндр можно разрезать и аккуратно разложить на плоскости (длины на цилиндре ведут себя точно также, как на плоскости).
Найдем координатные векторы  по формуле (10):
по формуле (10):

Для нахождения коэффициентов L, M, N второй квадратичной формы необходимо найти единичный вектор нормали 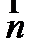 :
:


Найдем коэффициенты L, M, N второй квадратичной формы:

Таким образом, вторая квадратичная форма будет выглядеть следующим образом:

Найдем среднюю кривизну:

Найдем гауссову кривизну:

В данном случае (K= 0) можно сделать вывод, что перед нами цилиндрическая поверхность и гауссова кривизна цилиндра всегда равна 0.
Конус
Параметризация конуса (см. рис.5) выглядит следующим образом:  Реализацию программы построения цилиндра в параметрических координатах можно увидеть в приложении C.
Реализацию программы построения цилиндра в параметрических координатах можно увидеть в приложении C.
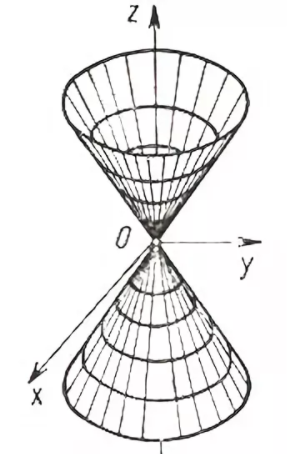
Рисунок 5 – Криволинейные координаты конуса
Найдем координатные векторы  и
и  по формуле (10):
по формуле (10):

Далее найдем коэффициенты E, F, G первой квадратичной формы:

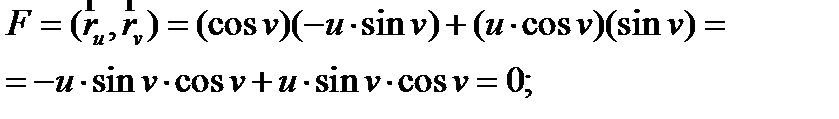

Таким образом, первая квадратичная форма будет выглядеть следующим образом:

Найдем координатные векторы  по формуле (10):
по формуле (10):

Для нахождения коэффициентов L, M, N второй квадратичной формы необходимо найти единичный вектор нормали 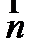 :
:


Найдем коэффициенты L, M, N второй квадратичной формы:


Таким образом, вторая квадратичная форма будет выглядеть следующим образом:

Найдем среднюю кривизну:

Найдем гауссову кривизну:

Так как перед нами представлен конус, то его гауссова кривизна будет всегда равна 0.
 2020-06-30
2020-06-30 310
310








