Решить дифференциальные уравнения. Найти частное решение (интеграл), если указаны начальные условия.
1. 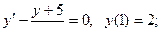
При решении любого дифференциального уравнения необходимо сначала ''увидеть'' к какому виду дифференциального уравнению оно относится.
Преобразуем дифференциальное уравнение 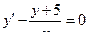 ,
, 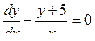 ,
,  - данное дифференциальное уравнение относится к виду дифференциальных уравнений 1-го порядка с разделяющимися переменными так как оно имеет вид
- данное дифференциальное уравнение относится к виду дифференциальных уравнений 1-го порядка с разделяющимися переменными так как оно имеет вид 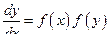 , где
, где 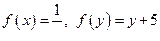 .
.
Разделяем переменные
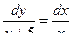 дифференциальное уравнение с разделенными переменными
дифференциальное уравнение с разделенными переменными
Интегрируем
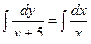 ,
,
 ,
,
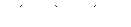
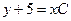 ,
,
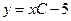 - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
Определяем произвольную константу C. Для этого подставляем начальные условия 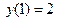 в общее решение.
в общее решение.
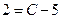 ,
, 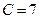 .
.
Подставляем 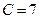 в общее решение.
в общее решение.
 - частное решение дифференциального уравнения.
- частное решение дифференциального уравнения.
Проверка:
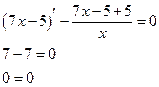
Получили тождество, значит наше решение найдено верно.
Ответ: 
2. 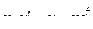 преобразуем дифференциальное уравнение
преобразуем дифференциальное уравнение
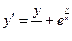 - имеем однородное дифференциальное уравнение первого порядка вида
- имеем однородное дифференциальное уравнение первого порядка вида 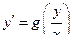 .
.
Делаем замену 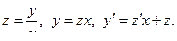 Подставляем замены в дифференциальное уравнение
Подставляем замены в дифференциальное уравнение

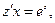
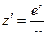 дифференциальное уравнение с разделяющимися переменными.
дифференциальное уравнение с разделяющимися переменными.
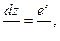
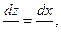
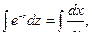


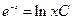 прологарифмируем обе части уравнения
прологарифмируем обе части уравнения  ,
,  .
.
Возвращаемся к замене
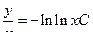 ,
,
 общее решение дифференциального уравнения
общее решение дифференциального уравнения
Проверка:
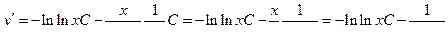
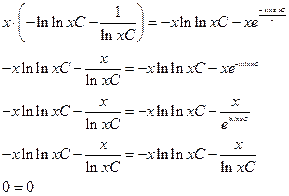
Получили тождество, значит наше решение найдено верно.
Ответ: 
3. 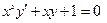 преобразуем дифференциальное уравнение
преобразуем дифференциальное уравнение
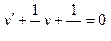 ,
, 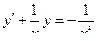 - дифференциальное уравнения вида
- дифференциальное уравнения вида  , где
, где 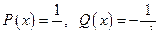 .
.
Сделаем замену
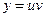 ,
, 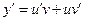 .
.
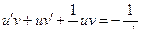 ,
,
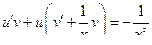 ,
,
1. 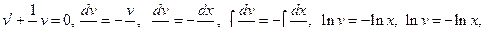
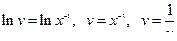 .
.
2. Подставим в выражение 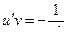 , найденное
, найденное 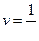 .
.
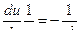 ,
, 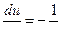 ,
, 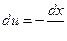 ,
, 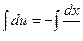 ,
, 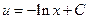 .
.
3. Найденные 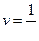 и
и 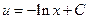 . Подставляем в
. Подставляем в 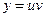 получаем
получаем 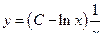 общее решение дифференциального уравнения.
общее решение дифференциального уравнения.
Проверка
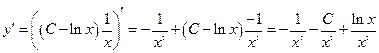

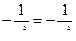
Получили тождество, значит наше решение найдено верно.
Ответ: 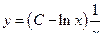
4. 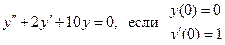 .
.
Уравнение вида 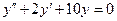 есть однородное дифференциальное уравнение второго порядка с постоянными коэффициентами вида
есть однородное дифференциальное уравнение второго порядка с постоянными коэффициентами вида  .
.
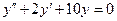
записываем характеристическое уравнение
 и решаем его как обычное квадратное уравнение.
и решаем его как обычное квадратное уравнение.

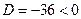 , следовательно, будем иметь комплексные корни.
, следовательно, будем иметь комплексные корни.
 ,
,  ,
, 
Общее решение для такого типа уравнений с мнимыми корнями имеет вид
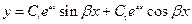
Для нашего случая
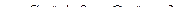 общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
Найдем частное решение
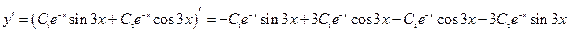
Подставляем начальные условия в общее решение 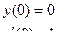 .
.
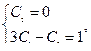
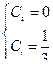
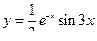 - частное решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
- частное решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
Проверка
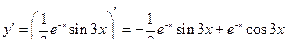 ,
,
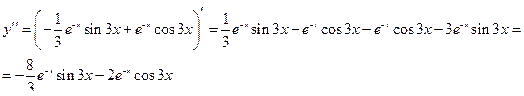
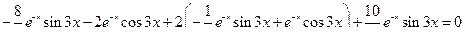
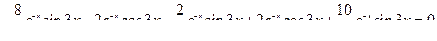
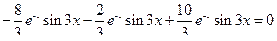
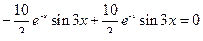
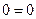
Ответ: 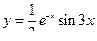 .
.
4. 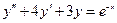 имеем дифференциальное уравнение второго порядка с постоянными коэффициентами.
имеем дифференциальное уравнение второго порядка с постоянными коэффициентами.
1. Сначала решают однородное дифференциальное уравнение
 ,
,
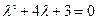 ,
,
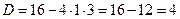 ,
,
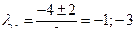 оба корня действительные.
оба корня действительные.
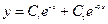 общее решение однородного дифференциального уравнения
общее решение однородного дифференциального уравнения
2. 
Сравниваем правую часть функции 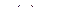 с её общим видом
с её общим видом 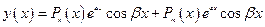 .
.
 будет равно
будет равно 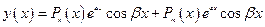 , если
, если
 поскольку есть одно совпадение с корнем
поскольку есть одно совпадение с корнем  , то
, то 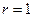 .
.
Определяем максимальную степень из многочленов  =>
=> 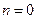 =>
=> 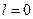 .
.
Следовательно,  .
.
Составляем макет частного решения неоднородного дифференциального уравнения
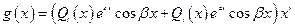 подставляя в него найденные коэффициенты
подставляя в него найденные коэффициенты
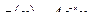 .
.
Пользуясь методом неопределенных коэффициентов определяем чему равен коэффициент 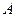 .
.
Находим производные

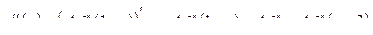
И подставляем данные производные в данное дифференциальное уравнение
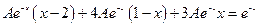
Сокращаем на 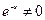
Приводим подобные и определяем коэффициент А.
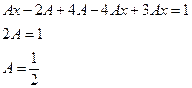
 .
.
В итоге общее решение неоднородного уравнения имеет вид
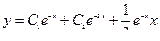 .
.
Проверка
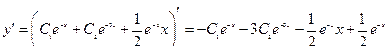
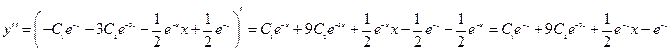
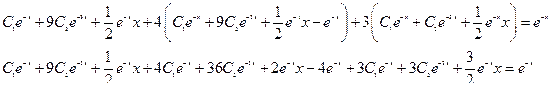
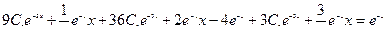
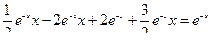
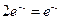
Ответ: 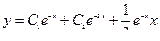
Задание №2
Решить систему дифференциальных уравнений с помощью характеристического уравнения.
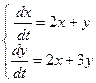
Решать систему уравнений будем самым распространенным методом - методом подстановки.
Продифференцируем выражение 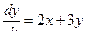 по переменной
по переменной 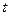 .
.
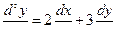 (1).
(1).
Первое уравнение системы  подставим в (1).
подставим в (1).
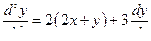
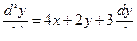
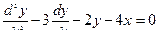 (2).
(2).
Из второго уравнения системы выразим x
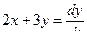 ,
,  и подставим его в уравнение (2).
и подставим его в уравнение (2).
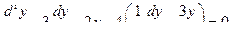
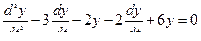
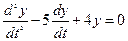 получили обычное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами в обычном штриховом виде которое имеет вид
получили обычное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами в обычном штриховом виде которое имеет вид
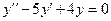 .
.
Составляем характеристическое уравнение
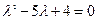
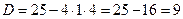
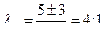 оба корня действительные.
оба корня действительные.
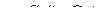 общее решение однородного дифференциального уравнения
общее решение однородного дифференциального уравнения
Для нахождения переменной х найдем 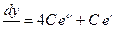 и подставим в
и подставим в 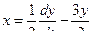 , получим
, получим

Ответ: 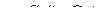 ,
, 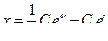 .
.
Ряды
Задание №3
Исследовать сходимость числовых рядов. Для знакопеременного ряда установить характер сходимости (абсолютная, условная).

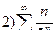
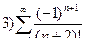
1. Проверим сходимость ряда 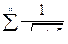 . Воспользуемся признаком Даламбера.
. Воспользуемся признаком Даламбера.
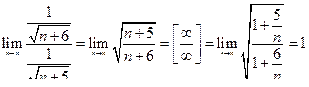 так как предел равен единице, то вопрос о сходимости ряда не решен. Будем искать другие признаки сходимости ряда.
так как предел равен единице, то вопрос о сходимости ряда не решен. Будем искать другие признаки сходимости ряда.
2. Воспользуемся интегральным признаком сходимости. Для того что пользоваться данным признаком необходимо выполнение двух условий.
Для данного ряда 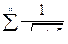 запишем ряд состоящий, например, из 4 слагаемых и сравним каждый член с предыдущим, получим
запишем ряд состоящий, например, из 4 слагаемых и сравним каждый член с предыдущим, получим
1)  то есть ряд убывает
то есть ряд убывает
2) 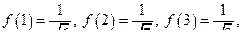 то есть
то есть 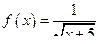 есть непрерывная и невозрастающая функция.
есть непрерывная и невозрастающая функция.
Два условия выполнены, следовательно, можно пользоваться интегральным признаком сходимости.
 так как несобственный интеграл не имеет предела, следовательно, ряд расходится.
так как несобственный интеграл не имеет предела, следовательно, ряд расходится.
2. Проверим сходимость ряда 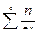 . Воспользуемся признаком Даламбера.
. Воспользуемся признаком Даламбера.
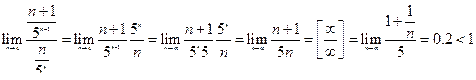 , следовательно,
, следовательно,
ряд сходится по признаку Даламбера.
3. Проверим сходимость ряда 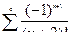 . Составим по данному ряду числовой ряд
. Составим по данному ряду числовой ряд
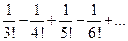 видно, что данный ряд знакопеременный. Для ответа на вопрос сходимости ряда воспользуемся признаком Лейбница
видно, что данный ряд знакопеременный. Для ответа на вопрос сходимости ряда воспользуемся признаком Лейбница
1. 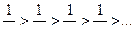 члены ряда убывают по абсолютной величине
члены ряда убывают по абсолютной величине
2. 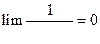 предел модуля общего члена ряда стремится к нулю, следовательно, данный ряд сходится по признаку Лейбница.
предел модуля общего члена ряда стремится к нулю, следовательно, данный ряд сходится по признаку Лейбница.
Проверим сходимость ряда по абсолютной величине 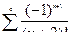 . То есть рассмотрим ряд
. То есть рассмотрим ряд
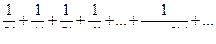 Для ответа на вопрос о сходимости ряда воспользуемся интегральным признаком сходимости.
Для ответа на вопрос о сходимости ряда воспользуемся интегральным признаком сходимости.
1) 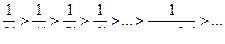 то есть ряд убывает
то есть ряд убывает
2) 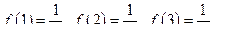 то есть
то есть 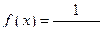 есть непрерывная и невозрастающая функция.
есть непрерывная и невозрастающая функция.
Два условия выполнены, следовательно, можно пользоваться интегральным признаком сходимости.
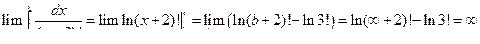 так как несобственный интеграл не имеет предела, следовательно, ряд расходится.
так как несобственный интеграл не имеет предела, следовательно, ряд расходится.
Так как знакопеременный ряд сходится, а ряд составленный из абсолютных членов ряда расходится, то ряд называется условно сходящимся.
Задание №4
Найти область сходимости степенного ряда.
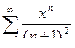
Запишем в развернутом виде сумму ряда
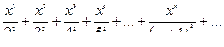
Найдем радиус сходимости степенного ряда 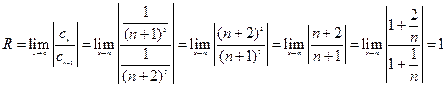
То есть интервал сходимости ряда 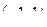
Выясним поведение ряда на концах интервала
При 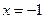 ряд принимает вид
ряд принимает вид
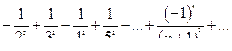
Так как ряд знакочередующийся, то для определения сходимости ряда используем признак Лейбница.
1. 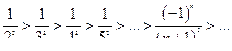 первое условие соблюдается
первое условие соблюдается
2. 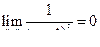 второе условие соблюдено, следовательно, ряд сходится по признаку Лейбница.
второе условие соблюдено, следовательно, ряд сходится по признаку Лейбница.
При 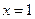 ряд принимает вид
ряд принимает вид
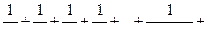
Для определения сходимости ряда используем, например, предельный признак сравнения.
Сравним данный ряд с обобщенным гармоническим рядом имеем
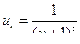 общий член данного ряда и
общий член данного ряда и 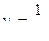 общий член обобщенного гармонического ряда, который сходится так как 2>1.
общий член обобщенного гармонического ряда, который сходится так как 2>1.
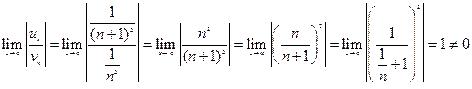 то данный ряд как и гармонический сходится.
то данный ряд как и гармонический сходится.
Ответ: 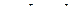
 2020-06-30
2020-06-30 101
101








