Практический (прямой) критерий статической устойчивости простейшей электрической системы

    Зададим кратковременное возмущение при работе в точке а:→ Ускорение:

Генератор вернется в точку а из-за торможения P_Э > P₀.

← Торможение:

Генератор ускорится и вернется в точку а, так как P_Э < P₀.

Таким образом точка а является точкой устойчивого режима.

Рассмотрим теперь точку b.

→ Ускорение:

В этом случае машина разгоняется и теряет устойчивость, так как P₀ > P_Э .

← Торможение:

Теперь машина будет тормозиться, так как  P_Э > P₀ и потеряет устойчивость

(переход к точке a).

    Режим работы в точке b не устойчив, а значит, невозможен.

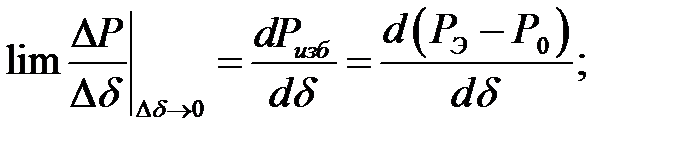
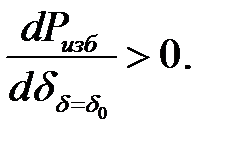                                                    Выражение (2.4) отражает практический или прямой критерий устойчивости.

Критерий устойчивости (2.4): если производная избыточной мощности

в точке исходного режима больше нуля, то электромеханическая система устойчива.

    Пример: P₀ = const (рис. 2.9);

                           

                                 Рис. 2.9. Зона устойчивости

90° > > 0°― зона устойчивости при P₀ = const.  ― система устойчива,

где  ― синхронизирующая мощность.

    Дифференциальный критерий устойчивости для этого частного случая переходит в интегральный 90° > > 0°― зона устойчивости при P₀ = const.

Упрощенные угловые характеристики мощности регулируемых систем.

Угловые характеристики регулируемых систем (упрощенные) и динамическая угловая характеристика мощности могут быть получены аналогично на основе векторной диаграммы (рис. 2.11). АРВ сильного действия. При UГ = const, xГ = 0:

― упрощенная угловая характеристика при АРВ сильного действия. АРВ пропорционального действия. При Еq = const, xГ = d х:

упрощенная угловая характеристика при АРВ пропорционального действия, где: dΣ d C x' x' x. Динамическая угловая характеристика мощности (используется при упрощенном анализе динамической устойчивости). При E’ = const, xГ = d х:

― динамическая характеристика (без учета электромагнитных переходных процессов).