Магнитный момент контура с током

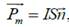
где 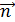 – положительная нормаль к плоскости контура – единичный вектор, направление которого связано с направлением тока в контуре правилом «правого винта»; I – сила тока в контуре; S – площадь контура.

Механический (вращающий) момент, действующий на контур с током, помещенный в однородное магнитное поле

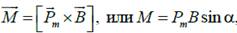
где α – угол между векторам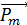и   и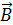

Потенциальная энергия контура с током в магнитной поле:

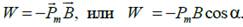
Сила Лоренца, действующая на заряд, движущийся в магнитном поле

Сила Лоренца:

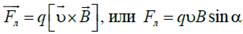
где υ – скорость заряженной частицы; α – угол между векторам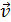и  и  .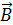

Направление силы Лоренца определяется по «правилу левой руки»: четыре пальца левой руки расположить по направлению скорости движения частицы, силовые линии должны входить в ладонь, тогда отогнутый на 90 большой палец покажет направление силы Лоренца.

Это сформулировано для положительного заряда, для отрицательного заряда направление силы Лоренца будет прямо противоположное.

Параметры винтовой траектории (радиус R, период Т обращения, шаг h), описываемой частицей в общем случае, когда частица влетает в магнитное поле под углом к силовым линиям поля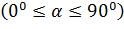

В случае, когда заряженная частица влетает перпендикулярно силовым линиям поля, она будет двигаться по окружности в плоскости, перпендикулярной силовым линиям поля.

Радиус траектории и период обращения заряда в поле равен

Работа по перемещению проводника с током в магнитном поле.

Магнитный поток

Поток вектора 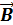 через контур площадью S:

а) в случае однородного магнитного поля и плоской поверхности

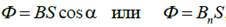
где S – площадь контура; α – угол между нормалью к плоскости контура и вектором магнитной индукции 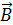 ; B_n – проекция вектора на направление нормали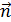

б) в случае неоднородного поля и произвольной поверхности

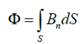
(интегрирование ведется по всей поверхности).

Потокосцепление – полный поток вектора 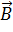 через N витков:

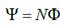
где Ф – магнитный поток через один виток; N – число витков тороида или соленоида

Работа по перемещению проводника или замкнутого контура с током I в магнитном поле

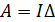
где 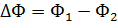 – изменение потока, проходящего через площадь контура, Ф₁, Ф₂ – магнитные потоки, пронизывающие плоскость контура в конечном (Ф₂) и начальном (Ф₁) состояниях.