Почему деление на ноль не определено?

0 был введен как часть большого механизма под названием целые числа для обозначения отсутствия чего-то. 0 облегчает счет и запись чисел, но нулевого количества нет, на него не укажешь пальцем, поэтому сказать, сколько 0 содержится в другом числе нельзя.

Разделить 3 на 0 означает сказать, сколько раз в 3 ничего нет. Ответить на вопрос, сколько в гараже квадратных метров можно, но ответить, сколько в нем пустоты, – нет.

Если бы был придуман какой-то смысл для выражения 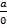, то это противоречило бы некоторым известным свойствам и определениям, например свойствам умножения, поэтому деление на 0 не определяют.

Можно все же попробовать разделить 3 на 0. Деление – это действие, обратное умножению, т.е. 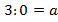, если .

Но при умножении на 0 всегда получается 0, т.е. такого просто не существует.

Рассмотрим случай деления 0 на 0, чтобы не возникало ощущения, что он – особый и отличается от деления 3 на 0.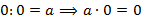

Равенство будет справедливым для любого , потому что Но результат деления должен быть конкретным числом. Снова получаем противоречие.

Поэтому деление на 0 в математике не определено.

Недопустимые значения переменных

Подставить в алгебраическое выражение можно любое число, но не всегда получится посчитать его значение.

Определение: такие значения переменной, при которых выражение не определено (нельзя вычислить его значение), называют недопустимыми значениями.

На данный момент мы знакомы только с одним таким случаем. Например, если в выражении есть дробь или деление 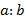, то мы не будем подставлять в выражение такие значения переменной, при которых знаменатель обращается в 0: .

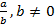Есть и другие случаи появления недопустимых значений переменных, но о них мы узнаем позже, по мере изучения различных функций.

Рассмотрим примеры на определение недопустимых значений переменных в выражениях.

Пример 1. Определить недопустимые значения переменной в выражении .

Решение. Выражение представляет собой дробь, поэтому её знаменатель не может обращаться в 0: .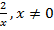

Таким образом, недопустимым значением переменной является 0, т.е. выражение определено для любых .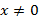

Ответ: 0.

Пример 2. Определить недопустимые значения переменной в выражении .

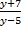Решение. Выражение 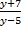представляет собой дробь, поэтому её знаменатель 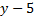не может обращаться в 0: .

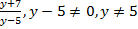Таким образом, недопустимым значением переменной является 5, т.е. выражение определено для любых .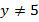

Ответ: 5.