2020-07-01
385
Найдем недопустимые значения переменных для выражения: 
.
Знаменатель дроби содержит переменные, определим, когда он обратится в 0:
Т.е. недопустимыми значениями переменных будут противоположные значения. Например, если 
, то 
.
Эквивалетность выражений
Выражения и 
не являются эквивалентными для любых 
и 
, т.к. первое выражение не определено, когда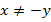 
, а второе выражение определено при любых значениях переменных и .
Т.е. эти выражения будут эквивалентными только для таких и , которые не являются противоположными числами.
Примеры упрощения алгебраических выражений
Задача 4. Упростите выражение: 
.
Решение. Воспользуемся распределительным законом, чтобы раскрыть обе скобки:
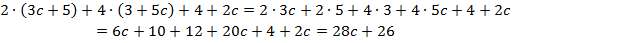
Ответ: 
.
Задача 5. Упростите выражение: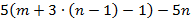 
.
Решение: воспользуемся распределительным законом, чтобы раскрыть внутренние скобки, затем упростим полученное в скобках выражение и снова применим распределительный закон:
Ответ: 
.
Всегда ли лучше упрощать выражение
Задача 1. Найдите значение выражения 
, если 
, 
.
|
|
|
Решение.
Вычисление с упрощением выражения (воспользуемся формулой разности квадратов, которая была записана ранее):
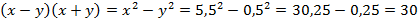
Вычисление без упрощения выражения:
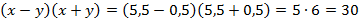
Ответ: 30.
В данном случае оказалось, что считать быстрее, если выражение не упрощать.
Таким образом, упрощать или не упрощать выражение, нужно решать в зависимости от условия и удобства решения конкретной задачи.
Задача 6. Пусть 
и 
– некоторые натуральные числа. Докажите, что разность чисел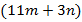 
и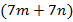 
делится на 4.
Доказательство
Рассмотрим разность чисел: 
.
Упростим выражение – раскроем скобки (помним, что минус перед скобками относится к обоим слагаемым в скобках):
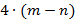делится на 
, значит, и эквивалентное ему исходное выражение делится на .
Доказано
Заключение
На этом уроке мы вспомнили, как работать с числовыми выражениями, и научились работать с алгебраическими выражениями. Мы научились находить допустимые и недопустимые значения переменных для выражений, содержащих дроби или деление, а также обсудили, что значит упростить алгебраическое выражение.
