Метод 1. Метод разложения на множители

Данный метод, используя знания школного курса математики, можно осуществить в нескольких вариантах, в зависимости от вида самого уравнения.

а) вынесение общего множителя за скобки

Задача 1. Решить уравнение: х² + 2ху = 4х + 7

Решение:   х² + 2ху - 4 х = 7,

Вынесем переменную х за скобки(х + 2 у - 4) х = 7

Так как все переменные могут принимать только целочисленные значения, то запишем все возможные целые делители числа 7.

7 = 7 ∙ 1 = 1 ∙ 7= (- 1) ∙ (- 7) = (- 7) ∙ (-1)

Получаем четыре системы уравнений

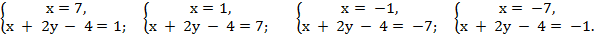
Тогда

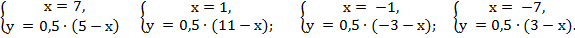
Или

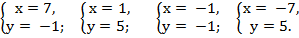
Ответ: (1; 5), (7; -1), (-1; -1), (-7; 5)

  б) применение формул сокращенного умножения 

Задача 2. Найдите все пары натуральных чисел, разность квадратов которых равна 33.

Решение. Запишем условие задачи в виде уравнения (х + у)(х - у) = 33

Так как все переменные могут принимать только натуральные значения, то запишем все возможные целые делители числа 33.

7 = 33 ∙ 1 = 1 ∙ 33= 11 ∙ 3 = 3∙ 11.

Учитывая, что сумма натуральных чисел всегда больше разности, то возможны только два варианта

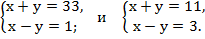
Решим системы методом сложения. Тогда получаем

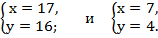
Ответ: (17; 16),  (7; 4),

в) способ группировки

Задача 3. Решить уравнение: xy - 2x + 3y = 16.

Решение:     (ху – 2х) + (3у – 6) = 10 или   х(у – 2) + 3у – 6 = 10 или

              х(у – 2) + 3(у – 2) = 10 или                    (х + 3)(у – 2) = 10

Так как все переменные могут принимать только целочисленные значения, то запишем все возможные целые делители числа 10.

10 = 10 ∙ 1 = 1 ∙ 10= (- 10) ∙ (- 1) = (- 1) ∙ (-10)  = 5 ∙ 2 = 2 ∙ 5= (- 2) ∙ (- 5) = (- 5) ∙ (- 2)

получаем восемь систем уравнений:

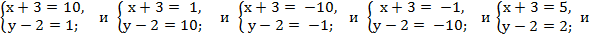
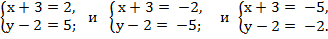
Решив полученные системы уравнений, получим:

  (7; 3), (-2; 12), (-1; 7), (2; 4), (-13; 1), (-4; -8),(-5; -3), (-8; 0)

 Ответ: (7; 3), (-2; 12), (-1; 7), (2; 4), (-13; 1), (-4; -8), (-5; -3), (-8; 0)

г) разложение квадратного трехчлена

Задача 4. Решить уравнение в целых числах:   х² - 5ху+4у²=13

Решение: Разложим трехчлен х ² - 5 ху + 4 у ² на множители, для этого решим уравнение 

х ² - 5 ху + 4 у ² = 0 относительно переменной х.

D = (- 5 у)² - 4∙1∙4 у ² = 25 у ² - 16 у ² = 9 у ². Тогда корни уравнения имеют вид:

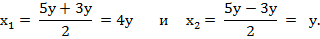
Теперь можно разложить левую часть уравнения на множители. Получаем 

(х – у)(х – 4 у)=13.

Так как все переменные могут принимать только целочисленные значения, то запишем все возможные целые делители числа 13

 13 = 1·13=13·1=(-1)·(-13)=(-13)·(-1).

Составим четыре системы уравнений:

 

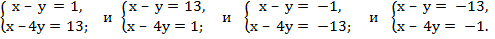
Решив полученные системы уравнений методом сложения, получим  пары чисел (-3; -4), (3; 4), (17;4), (-17;-4).

Ответ: (-3; -4), (3; 4), (17;4), (-17;-4)

д) использование параметра

Задача 5. Решите уравнение 2x²− 2xy + 9x + y = 2 в целых числах.

Решение.  Введем параметр а и перепишем уравнение в виде  2 x ² − (2 y − 9) x + y − 2 + a = a

 и разложим левую часть уравнения на множители как квадратный трехчлен относительно х (смотри предыдущий пример).

D = (2 y − 9)² - 4∙2∙ (у – 2 + а) = 4 y ² − 36 у + 81 -8 y + 16 −8 a = 4y² − 44y + 97 −8a.

Дискриминант будет полным квадратом, если 97 −8 a =121. Тогда D = (2у – 11)²,

 - 8а = 24 и a = −3.

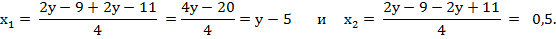
Теперь можно разложить левую часть уравнения на множители. Получаем 

2(х – 0,5)(х – у +5) или (2 x −1)(x − y + 5).

Уравнение принимает вид (2 x −1)(x − y + 5) = −3.

Так как все переменные могут принимать только целочисленные значения, то запишем все возможные целые делители числа – 3:

- 3 = 1·(- 3) = (- 1)·3 =  3·(- 1) = (- 3)·1

Из этого уравнения получим следующие системы уравнений:

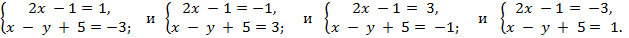
Решив эти системы, получим:

Ответ: (1;9); (0;2); (2;8); (−1;3).