10.4.1. Вычислить тройные интегралы:
а)  ; б)
; б)  , где
, где  – область, ограниченная плоскостями
– область, ограниченная плоскостями  ,
,  ,
,  и
и  ; в)
; в)  , где область
, где область  ограничена гиперболическим параболоидом
ограничена гиперболическим параболоидом  и плоскостями
и плоскостями  и
и  (
( ).
).
10.4.2. Вычислить при помощи тройного интеграла объем тела, ограниченного поверхностями: а)  ,
, 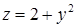 ,
,  ,
,  ; б)
; б)  ,
,  ,
,  ,
,  ,
,  ; в)
; в)  ;
;  ,
,  ,
,  ,
,  .
.
10.4.3. Найти центр масс однородного тела, ограниченного цилиндрами  ,
,  и плоскостями
и плоскостями 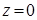 и
и  .
.
10.4.4. Вычислить массу тела, ограниченного прямым круговым цилиндром радиуса  и высоты
и высоты  , если его плотность в любой точке численно равна квадрату расстояния этой точки от центра основания цилиндра.
, если его плотность в любой точке численно равна квадрату расстояния этой точки от центра основания цилиндра.
Ответы. 10.4.1. а)  ; б)
; б) 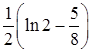 ; в)
; в)  . 10.4.2. а)
. 10.4.2. а)  ; б)
; б)  ; в)
; в)  . 10.4.3.
. 10.4.3. 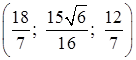 . 10.4.4.
. 10.4.4.  .
.
ЧАСТЬ Б)
(ДИСТАНЦИОННОЕ ОБУЧЕНИЕ)
ТРОЙНОЙ ИНТЕГРАЛ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
Тройной интеграл в цилиндрических и сферических координатах
Цилиндрические координаты — это  , где
, где  — аппликата точки, а
— аппликата точки, а  — полярные координаты проекции этой точки на координатную плоскость
— полярные координаты проекции этой точки на координатную плоскость  . Таким образом,
. Таким образом,  , а
, а  . Произведение дифференциалов при переходе от декартовых координат к цилиндрическим заменяется по правилу
. Произведение дифференциалов при переходе от декартовых координат к цилиндрическим заменяется по правилу  (ср. п. 9.2), а интегрирование обычно производится в таком порядке:
(ср. п. 9.2), а интегрирование обычно производится в таком порядке:
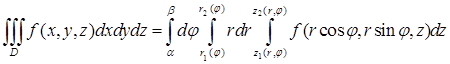 .
.
Здесь  и
и  — переписанные в цилиндрических координатах уравнения нижней
— переписанные в цилиндрических координатах уравнения нижней  и верхней
и верхней  границ области интегрирования
границ области интегрирования  (рис. 10.1), т. е.
(рис. 10.1), т. е.  ,
, 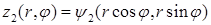 .
.

|
| Рис. 11.1 |
Сферические координаты для точки с декартовыми координатами  определяются так:
определяются так:  — расстояние от начала отсчета до этой точки,
— расстояние от начала отсчета до этой точки,  — угол между проекцией радиус-вектора точки на плоскость
— угол между проекцией радиус-вектора точки на плоскость 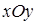 и осью
и осью  и
и  — угол между радиус-вектором точки и осью
— угол между радиус-вектором точки и осью  (см. рис. 11.1). Связь между декартовыми и сферическими координатами точки выражается формулами:
(см. рис. 11.1). Связь между декартовыми и сферическими координатами точки выражается формулами:
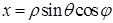 ,
,  ,
,  . Произведение дифференциалов при переходе к сферическим координатам заменяется по правилу
. Произведение дифференциалов при переходе к сферическим координатам заменяется по правилу
 .
.
Очевидно, что  ,
,  ,
,  (или
(или 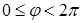 ). Предпочтительный порядок интегрирования — внутреннее по
). Предпочтительный порядок интегрирования — внутреннее по  , промежуточное по
, промежуточное по  и внешнее по углу
и внешнее по углу  :
:
 .
.
Заметим, что иногда угол  отсчитывают не от оси
отсчитывают не от оси  , а от плоскости
, а от плоскости  . Тогда
. Тогда 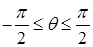 , и во всех приведенных формулах надо заменить
, и во всех приведенных формулах надо заменить  на
на 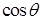 , а
, а  — на
— на  .
.
 2020-06-29
2020-06-29 119
119








