2020-06-29
76
12.3.1. Вычислить площадь той части поверхности 
, которая находится над прямоугольником, лежащим в плоскости 
и ограниченным прямыми 
, 
, 
, 
.
Решение. Найдем элемент площади поверхности: 
. Теперь легко найдем искомую площадь: 
.
12.3.2. Вычислить площадь части параболоида 
, вырезанной цилиндром 
.
Решение. Поверхность задана уравнением 
, отсюда 
. Двойной интеграл, выражающий площадь, равен 
. Для его вычисления перейдем к полярным координатам: 
.
12.3.3. Вычислить часть поверхности конуса 
, отсекаемую цилиндром 
.
Решение. В этом примере надо найти часть поверхности конуса, лежащую над кругом 
радиуса 
. Площадь круга равна 
. Вычислим элемент поверхности конуса:
, 
.
12.3.4. Вычислить площадь части земной поверхности, считая ее сферой радиуса 
км, заключенной между меридианами 
, 
и параллелями 
и 
.
Решение. Используя приведенную в пункте 12.1 формулу элемента площади в сферических координатах для сферы с уравнением 
, получим 
. Следует учесть, однако, (ср. замечание в пункте 11.1), что географическая широта 
и угол 
связаны соотношением 
, поэтому в нашем примере 
и 
. Отсюда
км2.
12.3.5. Вычислить интеграл 
, где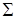 
– полная поверхность конуса при 
.
Решение. И боковая поверхность конуса, и его основание имеют одну и ту же проекцию на плоскость 
, а именно: круг радиуса 
, заданный неравенством 
. Поэтому будем вычислять поверхностный интеграл отдельно для основания и для боковой поверхности. На основании 
, поэтому интеграл равен 
. Для боковой поверхности элемент площади равен 
(см. пример 12.3.3). Функция интегрирования 
на боковой поверхности равна 
, отсюда поверхностный интеграл равен
. Интеграл по всей поверхности получим сложением: 
.
12.3.6. Вычислить интеграл 
, где 
– поверхность тетраэдра 
, 
, 
, 
.
Решение. Поверхность тетраэдра состоит из четырех граней, интеграл по каждой из которых будем вычислять отдельно. Грань, лежащая в плоскости 
, проектируется на плоскость 
в треугольник, ограниченный осями 
, 
и прямой 
. Уравнение поверхности этой грани 
, откуда 
. Таким образом, поверхностный интеграл по этой грани равен 
.
Оставшиеся три грани расположены в координатных плоскостях. Для грани, расположенной в плоскости , 
, поэтому 
. Интегралы 
и 
по плоскостям 
и 
равны.
Найдем, например 
. Здесь мы учли, что на плоскости 
и что 
. Теперь найдем окончательный ответ:
.
12.3.7. Вычислить 
, где — часть плоскости 
, отсеченная координатными плоскостями.
Решение. Из уравнения плоскости удобнее выразить 
, тогда элемент площади поверхности равен 
. Проекция поверхности на координатную плоскость 
является треугольником 
, ограниченным прямой 
и осями координат. Запишем соответствующий двойной интеграл: 
.
12.3.8. Найти координаты центра масс восьмой части однородной сферы 
, , , .
Решение. Очевидно, в силу симметричности координаты 
, 
и 
центра масс восьмой части сферы в указанной системе координат совпадают, поэтому найдем значение аппликаты. Воспользуемся выражением элемента площади сферы, вычисленным в пункте 12.1: 
.
Здесь было учтено, что проекция 
восьмой части сферы на плоскость 
является четвертью круга и имеет площадь 
. Итак, центр масс находится в точке 
.
