2020-06-29
75
Не вдаваясь в строгое определение поверхностного интеграла первого рода, можно сказать, что оно аналогично определению двойного интеграла, только разбиению подвергается не плоская фигура 
, а поверхность 
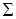в пространстве. Пусть 
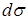— элемент площади поверхности 
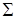, тогда поверхностный интеграл первого рода запишем в виде 
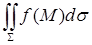. Здесь точка 
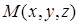принадлежит поверхности 
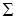. Интеграл 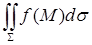сводят к двойному интегралу по проекции поверхности 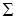на одну из координатных плоскостей, например, на плоскость 
. Подставляя выражение для элемента площади поверхности и учитывая, что на 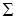координата 
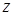зависит от 
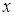и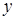 
(заменяем 
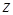на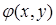 
), получим:
.
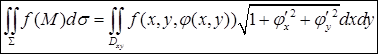Основные свойства поверхностного интеграла первого рода аналогичны свойствам двойного интеграла.
При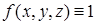 
интеграл 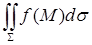дает площадь поверхности 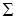. Если 
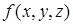— поверхностная плотность (масса единицы площади поверхности), то этот интеграл дает полную массу поверхности 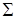. Среднее арифметическое функции 
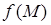на поверхности 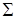выражается формулой
.
