Консультация к экзамену (1 час)
Письменный экзамен состоит из 10 заданий. Сегодня разберем первые 7 заданий. Задания перепишите в тетрадь. Завтра разберем геометрические задачи и задания по теории вероятности (задания 8-10)
Задание 1 – Задача на проценты
Пример 1: Цену на автомобиль «Волга» снизили сначала на 20%, а затем ещё на 15%. При этом он стал стоить 238000 рублей. Какова была первоначальная цена автомобиля?
Решение.
Пусть первоначальная стоимость автомобиля равна х рублей.
х∙(1-0,2)∙(1-0,15)=238000
0,8∙0,85∙х=238000
0,68∙х=238000
х=238000:0,68
х=350000 (первоначальная цена автомобиля)
Ответ: 350000 рублей.
Пример 2: Только 94% из 27500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу В1?
Решение.
27500чел. – 100%
х чел. – 94%
х=27500∙94:100=25850(чел.)
Ответ: 25850 выпускников.
Задание - Вычисление арифметических выражений на свойства степени и корня п-ой степени
Пример 1: Найдите значение выражения 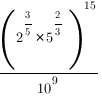
Разложим число 10 в знаменателе дроби на простые множители и воспользуемся свойствами степеней:
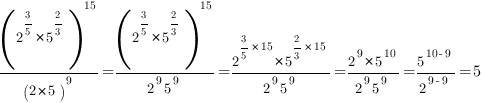
Пример 2: Найдите значение выражения 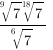 .
.
Запишем корни в виде степени и воспользуемся свойствами степеней с одинаковым основанием:
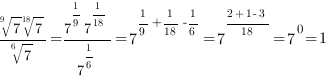
Ответ: 1.
Задание - вычисление тригонометрических выражений
Пример:. Найдите значения тригонометрических функций числа 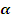 , зная, что
, зная, что 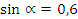 и
и 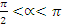 .
.
Решение:
Так как по условию 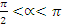 , то
, то 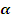 - принадлежит II четверти. Поэтому
- принадлежит II четверти. Поэтому
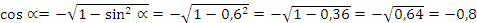 ;
;
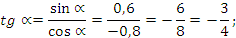
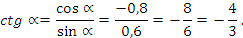
задание – Решение логарифмических уравнений
Пример 1. Решите уравнение 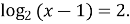
Решение. По определению логарифма имеем 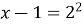 . Отсюда х =3.
. Отсюда х =3.
Число 3 входит в область определения, следовательно, является корнем данного уравнения.
Ответ: 3
Пример 2. Найдите корень уравнения 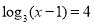 .
.
Решение. По определению логарифма получаем: 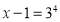
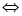
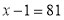
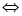
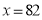 . Число 82 входит в область определения (82 – 1>0), следовательно, является корнем уравнения.
. Число 82 входит в область определения (82 – 1>0), следовательно, является корнем уравнения.
Ответ: 82
Пример 3. Найдите корень уравнения 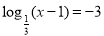 .
.
Решение. Последовательно получаем: 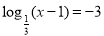
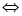
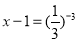
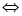
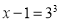
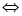
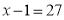
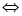
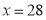 . Число 28 входит в область определения (28 – 1=27>0), значит, является решением уравнения.
. Число 28 входит в область определения (28 – 1=27>0), значит, является решением уравнения.
Ответ: 28
Пример 4. Решите уравнение 2lg(x – 1)=lg(5 x +1).
Решение. По свойствам логарифма данное уравнение равносильно уравнению (х – 1)2=5 х +1.
х 2 – 2 х +1=5 х +1; х 2 – 7 х =0; х (х ‑ 7)=0. Отсюда х =0 и х =7.
Число 0 не входит в область определения
Ответ: 7
5 задание – Решение показательных неравенств
Пример №1. Решить неравенство: 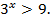
Правило: привести к одинаковому основанию.
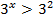
Так как основание больше 1, знак неравенства не меняется 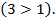
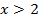
Ответ: 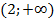
Пример 2: Решить неравенство: 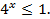
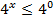
Так как основание больше 1, знак неравенства не меняется 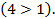
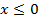
Ответ: 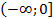
Пример 3: Решить неравенство: 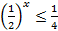
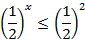
Так как основание меньше 1, знак неравенства меняется 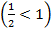
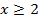
Ответ: 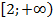
Пример 4: 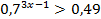
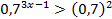
Так как основание меньше 1, знак неравенства меняется 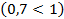
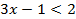
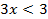
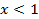
Ответ: 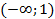
Пример 5: Решите неравенство 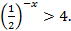
Рассмотрим решение данного неравенства двумя способами.
1 способ:
Приведем обе части неравенства к основанию 2: 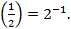
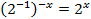
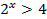
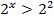
Так как основание больше 1, знак неравенства не меняется 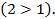
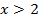
2 способ:
Приведем обе части неравенства к основанию  :
: 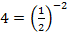
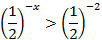
Так как основание меньше 1, знак неравенства меняется 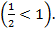
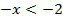
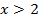
Ответ: 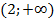
6 задание – Вычисление производной функции и её физический смысл
Пример 1
Вычислить производную функции 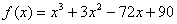 в точке
в точке 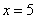
Решение: 1.Находим производную функции:
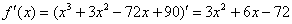
2.Вычислим значение производной в точке 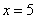 :
:
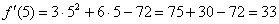
Ответ: 33
Пример 2. Точка движется прямолинейно по закону 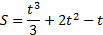 (S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.
(S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.
Решение:
скорость прямолинейного движения равна производной пути по времени, то есть 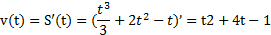 .
.
Подставив в уравнение скорости t=3 с, получим v(3)=32+4∙3-1= 20 (м/с).
Ответ: 20 м/c.
 2020-07-12
2020-07-12 131
131







