Пусть 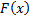 – первообразная для
– первообразная для 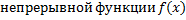 на
на 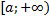 , тогда
, тогда
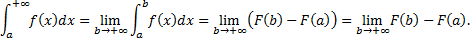
Таким образом, 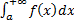 сходится
сходится 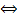
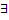 конечный предел первообразной
конечный предел первообразной 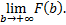
Примеры.
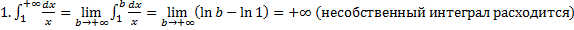 ,
, 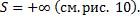
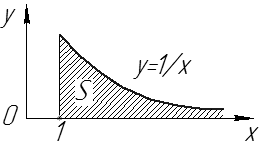
Рис. 10

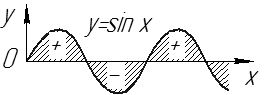
Рис. 11
3. 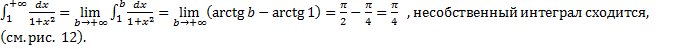
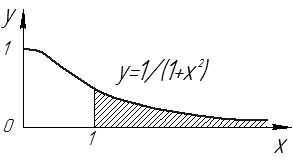
Рис. 12
4. 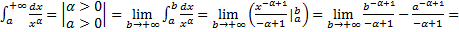
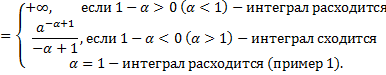
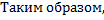
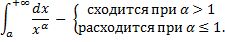
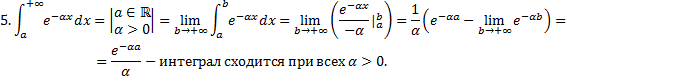
Исследование несобственных интегралов 1-го рода на сходимость.
| Рис. 13 |
 Признаки сходимости:
Признаки сходимости:
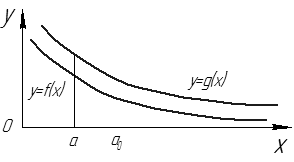
1. Признак сравнения.
Пусть 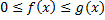
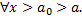
a. Если 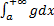 сходится, то
сходится, то 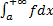 также сходится (см. рис. 13).
также сходится (см. рис. 13).
b. Если 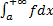 расходится, то
расходится, то 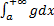 также расходится.
также расходится.
2. Предельный признак сравнения:
пусть для 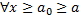
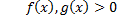 и
и 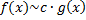 при
при 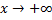 , т.е.
, т.е. 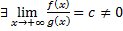 .
.
Тогда 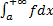 и
и 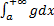 оба сходятся или оба расходятся.
оба сходятся или оба расходятся.
3. Если сходится 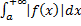 , то сходится и
, то сходится и 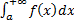 (обратное неверно!).
(обратное неверно!).
В качестве «образцов» интегралов для сравнения обычно используются интегралы
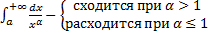 (a>0).
(a>0).
Примеры.
1. 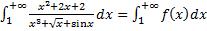 .
.
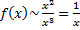 при
при 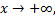
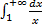 расходится
расходится 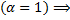 исходный интеграл расходится по предельному признаку.
исходный интеграл расходится по предельному признаку.
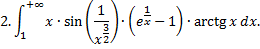
При 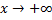
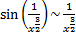 ;
; 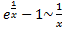 ;
; 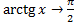 ,
,
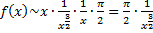 ;
; 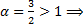 интеграл сходится по предельному признаку.
интеграл сходится по предельному признаку.
3. 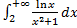
Т.к. при 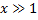
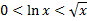 (логарифм растет медленней степенной функции), то
(логарифм растет медленней степенной функции), то 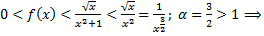 исходный интеграл сходится по признаку сравнения.
исходный интеграл сходится по признаку сравнения.
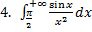 .
.
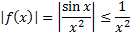
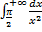 – сходится
– сходится 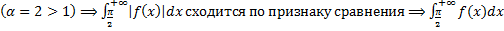 сходится по признаку 3.
сходится по признаку 3.
Несобственные интегралы 2-го рода
| Рис. 14 |
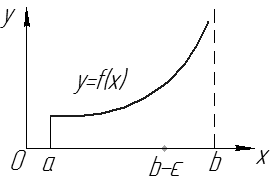 Пусть
Пусть  непрерывна на
непрерывна на 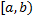 , но не ограничена в левой окрестности точки
, но не ограничена в левой окрестности точки 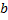 . Определенный интеграл
. Определенный интеграл 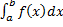 не существует, т.к.
не существует, т.к.  – неограниченная. Рассмотрим
– неограниченная. Рассмотрим 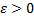 . Т.к.
. Т.к.  непрерывна на
непрерывна на 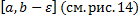 , то
, то 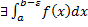 – определенный интеграл.
– определенный интеграл.
Опр. Несобственным интегралом 2 рода по 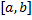 от функции
от функции  , неограниченной в окрестности точки
, неограниченной в окрестности точки 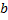 , называется предел
, называется предел
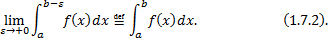
Если существует конечный предел (1.8.2), то несобственный интеграл 2-го рода называется сходящимся, в противном случае – расходящимся.
Геометрический смысл:
при 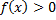 – площадь фигуры, ограниченной линиями
– площадь фигуры, ограниченной линиями 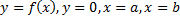 (см. рис. 15).
(см. рис. 15).
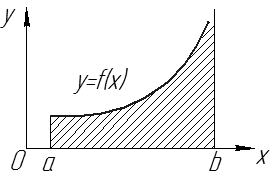
Рис. 15
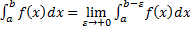 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 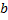 .
.
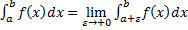 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 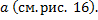
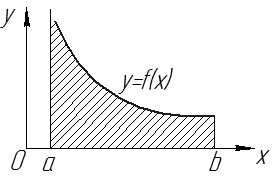
Рис. 16
Свойство линейности.
Если 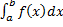 ,
, 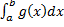 сходятся, то сходятся интегралы
сходятся, то сходятся интегралы
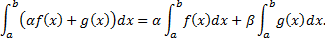
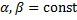 .
.
 2020-07-12
2020-07-12 163
163








